题目内容
将一个矩形纸片ABCD沿AD和BC的中点的连线对折,要使矩形AEFB与原矩形相似,则原矩形的长和宽的比应为
- A.2:1
- B.
 :1
:1 - C.
 :1
:1 - D.1:1
C
分析:设矩形ABCD的长AD=x,宽AB=y,根据相似多边形对应边的比相等,即可求得.
解答: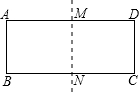 解:设矩形ABCD的长AD=x,宽AB=y,则DM=
解:设矩形ABCD的长AD=x,宽AB=y,则DM= AD=
AD= x.
x.
又矩形DMNC与矩形ABCD相似.
∴ =
= ,即
,即 =
=
即y2= x2.
x2.
∴x:y= :1.
:1.
故选C.
点评:本题主要考查了相似多边形的对应边的比相等,注意分清对应边是解决本题的关键.
分析:设矩形ABCD的长AD=x,宽AB=y,根据相似多边形对应边的比相等,即可求得.
解答:
 解:设矩形ABCD的长AD=x,宽AB=y,则DM=
解:设矩形ABCD的长AD=x,宽AB=y,则DM= AD=
AD= x.
x.又矩形DMNC与矩形ABCD相似.
∴
 =
= ,即
,即 =
=
即y2=
 x2.
x2.∴x:y=
 :1.
:1.故选C.
点评:本题主要考查了相似多边形的对应边的比相等,注意分清对应边是解决本题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目






 的大小关系.
的大小关系.


