题目内容
如图,双曲线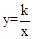 经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为5,则k的值是 ▲ .
经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为5,则k的值是 ▲ .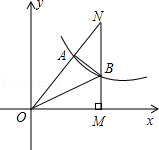
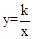 经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为5,则k的值是 ▲ .
经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为5,则k的值是 ▲ .
12。
反比例函数综合题。
【分析】如图,过A点作AC⊥x轴于点C,则AC∥NM,

∴△OAC∽△ONM,∴OC:OM=AC:NM=OA:ON。
又∵OA=2AN,∴OA:ON=2:3。
设A点坐标为(x0,y0),则OC=x0,AC=y0。
∴OM= ,NM=
,NM= 。∴N点坐标为(
。∴N点坐标为( ,
, )。
)。
∴点B的横坐标为 ,设B点的纵坐标为yB,
,设B点的纵坐标为yB,
∵点A与点B都在 图象上,∴k=x0 •y0=
图象上,∴k=x0 •y0= •yB。∴
•yB。∴ 。
。
∴B点坐标为( )。
)。
∵OA=2AN,△OAB的面积为5,∴△NAB的面积为 。∴△ONB的面积=
。∴△ONB的面积= 。
。
∴ ,即
,即 。∴
。∴ 。∴k=12。
。∴k=12。
【分析】如图,过A点作AC⊥x轴于点C,则AC∥NM,

∴△OAC∽△ONM,∴OC:OM=AC:NM=OA:ON。
又∵OA=2AN,∴OA:ON=2:3。
设A点坐标为(x0,y0),则OC=x0,AC=y0。
∴OM=
 ,NM=
,NM= 。∴N点坐标为(
。∴N点坐标为( ,
, )。
)。∴点B的横坐标为
 ,设B点的纵坐标为yB,
,设B点的纵坐标为yB,∵点A与点B都在
 图象上,∴k=x0 •y0=
图象上,∴k=x0 •y0= •yB。∴
•yB。∴ 。
。∴B点坐标为(
 )。
)。∵OA=2AN,△OAB的面积为5,∴△NAB的面积为
 。∴△ONB的面积=
。∴△ONB的面积= 。
。∴
 ,即
,即 。∴
。∴ 。∴k=12。
。∴k=12。
练习册系列答案
相关题目
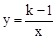 图象的两个分支分别位于第一、第三象限.
图象的两个分支分别位于第一、第三象限.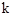 的取值范围;
的取值范围;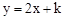 的图象与该反比例函数的图象有一个交点的纵坐标是4.
的图象与该反比例函数的图象有一个交点的纵坐标是4.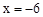 时反比例函数
时反比例函数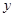 的值;
的值;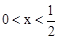 时,求此时一次函数
时,求此时一次函数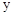 的取值范围.
的取值范围. 的图象上一点,则m=_______.
的图象上一点,则m=_______. (k≠0)经过点A,连结OA,设OA与x轴的夹角为
(k≠0)经过点A,连结OA,设OA与x轴的夹角为 .
.
 的图象与反比例函数
的图象与反比例函数 (
( )的图象交于
)的图象交于 、
、 两点。
两点。 为何值时,
为何值时, ?
?  (
( >0)的图像上,有点P1、P2、P3 、P4 ,它们的横坐标依次是1、2、3、4,分别过这些点作
>0)的图像上,有点P1、P2、P3 、P4 ,它们的横坐标依次是1、2、3、4,分别过这些点作 轴的垂线,图中所构成的阴影部分面积从左到右依次为S1、S2、S3,则S1+S2+S3的值为 ( ).
轴的垂线,图中所构成的阴影部分面积从左到右依次为S1、S2、S3,则S1+S2+S3的值为 ( ).
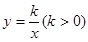 经过A、E两点,若AC:OB=1:3,梯形AOBC面积为24,则k=( )
经过A、E两点,若AC:OB=1:3,梯形AOBC面积为24,则k=( )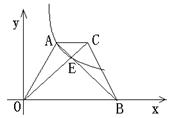
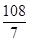 B、
B、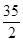 C、
C、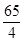 D、
D、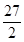
 与
与 (a≠0)在同一直角坐标系中的图象可能是( )
(a≠0)在同一直角坐标系中的图象可能是( )
 的图像交于P、Q两点,则线段PQ长的最小值是 .
的图像交于P、Q两点,则线段PQ长的最小值是 .