题目内容
当m为整数时,关于x的方程(2m-1)x2-(2m+1)x+1=0是否有有理根?如果有,求出m的值;如果没有,请说明理由.
当m为整数时,关于x的方程(2m-1)x2-(2m+1)x+1=0没有有理根.理由如下:
①当m为整数时,假设关于x的方程(2m-1)x2-(2m+1)x+1=0有有理根,则要△=b2-4ac为完全平方数,而△=(2m+1)2-4(2m-1)=4m2-4m+5=(2m-1)2+4,
设△=n2(n为整数),即(2m-1)2+4=n2(n为整数),所以有(2m-1-n)(2m-1+n)=-4,
∵2m-1与n的奇偶性相同,并且m、n都是整数,所以
或
,
解得m=
或m=-
(都不合题意舍去).
②2m-1=0时,m=
(不合题意舍去).
所以当m为整数时,关于x的方程(2m-1)x2-(2m+1)x+1=0没有有理根.
①当m为整数时,假设关于x的方程(2m-1)x2-(2m+1)x+1=0有有理根,则要△=b2-4ac为完全平方数,而△=(2m+1)2-4(2m-1)=4m2-4m+5=(2m-1)2+4,
设△=n2(n为整数),即(2m-1)2+4=n2(n为整数),所以有(2m-1-n)(2m-1+n)=-4,
∵2m-1与n的奇偶性相同,并且m、n都是整数,所以
|
|
解得m=
| 1 |
| 2 |
| 1 |
| 2 |
②2m-1=0时,m=
| 1 |
| 2 |
所以当m为整数时,关于x的方程(2m-1)x2-(2m+1)x+1=0没有有理根.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
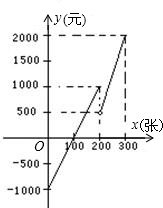 某游乐场每天的赢利额y(元)与售出的门票x(张)之间的函数关系如图所示.
某游乐场每天的赢利额y(元)与售出的门票x(张)之间的函数关系如图所示.