Question

【题目】（1）阅读：若一个三角形的三边长分别为a、b、c，设，

则这个三角形的面积为．

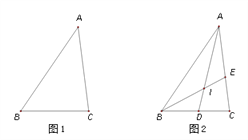
（2）应用：如图1，在△ABC中，AB=6，AC=5，BC=4，求△ABC面积．

（3）引申：如图2，在（2）的条件下，AD、BE分别为△ABC的角平分线，它们的交点为I，求I到AB的距离．

Answer 1

【答案】 (2) ;(3) ．

【解析】试题分析：（2）先根据三边长度求出p的值，再代入公式计算可得；

（3）过点I作IF⊥AB、IG⊥AC、IH⊥BC，由角平分线性质可得IF=IH=IG，再根据S△ABC=S△ABI+S△ACI+S△BCI即可求得IF的长．

试题解析：（1）如图：

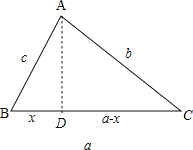
在△ABC中，过A作高AD交BC于D，

设BD=x，那么DC=a-x，

由于AD是△ABD、△ACD的公共边h2=c2-x2=b2-（a-x）2，

解出x得x=，

于是h=，

△ABC的面积S=ah=a

即S=a

令p=（a+b+c），

对被开方数分解因式，并整理得到s＝；

（2）由题意，得：a=4，b=5，c=6；

∴p= =；

∴S=，

故△ABC的面积是；

（3）如图，过点I作IF⊥AB、IG⊥AC、IH⊥BC，垂足分别为点F、G、H，

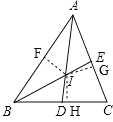
∵AD、BE分别为△ABC的角平分线，

∴IF=IH=IG，

∵S△ABC=S△ABI+S△ACI+S△BCI，

即，

∴3IF+IF+2IF=，

解得IF=，

故I到AB的距离为．