题目内容
点P在直线y=x上,OP=3 ,点B在x轴正半轴上,点A在y轴上,若OA=2,PA⊥PB,则点B的坐标为________.
,点B在x轴正半轴上,点A在y轴上,若OA=2,PA⊥PB,则点B的坐标为________.
(4,0)或(8,0)
分析:分当A在y轴的正半轴时,当A在y轴的负半轴时两种情况进行讨论,两种情况下P一定在第一象限,作PN⊥x轴于N,作PM⊥y轴于M,易证△APM≌△BPN,即可求得OB的长,则B的坐标可以求得.
解答: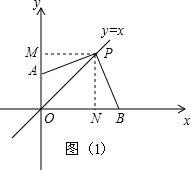 解:当A在y轴的正半轴时,P一定在第一象限,如图(1).
解:当A在y轴的正半轴时,P一定在第一象限,如图(1).
作PN⊥x轴于N,作PM⊥y轴于M.
则PM=PN= OP=3.
OP=3.
故OM=ON=PN=PM=3,
∵∠MPN=∠APB=90°,即∠APN+∠MPA=∠APN+∠BPN,
∴∠MPA=∠BPN,
在△APM和△BPN中,
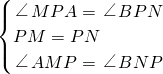 ,
,
∴△APM≌△BPN(ASA),
∴AM=BN=3-2=1,
∴OB=ON+BN=3+1=4,
 故B的坐标是(4,0);
故B的坐标是(4,0);
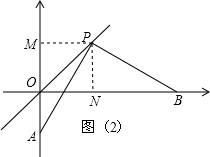
当A在y轴的负半轴时,如图(2).
同理可证△APM≌△BPN,
∴BN=AM=3+2=5,
∴OB=ON+BN=3+5=8.
故B的坐标是(8,0).
故答案是:(4,0)或(8,0).
点评:本题考查了全等三角形的判定与性质以及求点的坐标,正确进行讨论是关键.
分析:分当A在y轴的正半轴时,当A在y轴的负半轴时两种情况进行讨论,两种情况下P一定在第一象限,作PN⊥x轴于N,作PM⊥y轴于M,易证△APM≌△BPN,即可求得OB的长,则B的坐标可以求得.
解答:
 解:当A在y轴的正半轴时,P一定在第一象限,如图(1).
解:当A在y轴的正半轴时,P一定在第一象限,如图(1).作PN⊥x轴于N,作PM⊥y轴于M.
则PM=PN=
 OP=3.
OP=3.故OM=ON=PN=PM=3,
∵∠MPN=∠APB=90°,即∠APN+∠MPA=∠APN+∠BPN,
∴∠MPA=∠BPN,
在△APM和△BPN中,
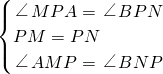 ,
,∴△APM≌△BPN(ASA),
∴AM=BN=3-2=1,
∴OB=ON+BN=3+1=4,
 故B的坐标是(4,0);
故B的坐标是(4,0);当A在y轴的负半轴时,如图(2).
同理可证△APM≌△BPN,
∴BN=AM=3+2=5,
∴OB=ON+BN=3+5=8.
故B的坐标是(8,0).
故答案是:(4,0)或(8,0).
点评:本题考查了全等三角形的判定与性质以及求点的坐标,正确进行讨论是关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

 (2010•郑州模拟)如图.点A的坐标为(-2.0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为
(2010•郑州模拟)如图.点A的坐标为(-2.0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为 (2012•广元)如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
(2012•广元)如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( ) (2012•淮北模拟)已知反比例函数
(2012•淮北模拟)已知反比例函数