题目内容
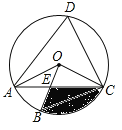
【题目】(1)如图1,OC平分∠AOB,点P在OC上,若⊙P与OA相切,那么⊙P与OB位置关系是 .

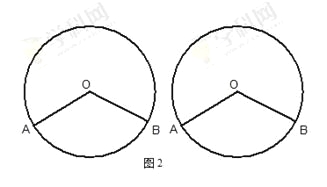
(2)如图2,⊙O的半径为2,∠AOB=120°,
①若点P是⊙O上的一个动点,当PA=PB时,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,求出⊙Q的半径; 如果不存在,请说明理由.
②若点P在BO的延长线上,且满足PA⊥PB,是否存在⊙Q,同时与射线PA.PB相切且与⊙O相切,如果存在,请直接写出⊙Q的半径; 如果不存在,请说明理由.
【答案】(1)相切;(2)①存在,半径可以为![]() ,4 ,
,4 ,![]() ,
,![]() ;②存在.其半径可以为1,
;②存在.其半径可以为1,![]() .
.
【解析】
试题(1)作PD⊥OA于A,PE⊥OB于B,则根据角平分线定义得到PD=PE,根据切线的性质由⊙P与OA相切得到PD为⊙P的半径,然后根据切线的判定定理可得到OB为⊙P的切线;
(2)①由PA=PB得到点P为∠AOB的平分线或反向延长线与⊙O的交点,分类讨论:当P点在优弧AB上时,当P点在劣弧AB上时,然后解四个方程即可得到满足条件的⊙Q的半径;
②作QH⊥PB于H,由PA⊥PB得∠APB=90°,由⊙Q与射线PA.PB相切,根据切线的性质得PQ平分∠APB,即∠QPH=45°,所以QH=PH,在Rt△POA中易得OP=1,设⊙Q的半径为r,即PH=QH=r,则OH=PH﹣OP=r﹣1,在Rt△OQH中,根据勾股定理得OQ2=OH2+QH2=(r﹣1)2+r2,
若⊙Q与⊙O内切时,OQ=2﹣r,得到(2﹣r)2=(r﹣1)2+r2,若⊙Q与⊙O外切时,OQ=2+r,得到(2+r)2=(r﹣1)2+r2,然后解两个方程即可得到满足条件的⊙Q的半径.
试题解析:(1)作PD⊥OA于A,PE⊥OB于B,如图1,
∵OC平分∠AOB,
∴PD=PE,
∵⊙P与OA相切,
∴PD为⊙P的半径,
∴PE为⊙的半径,
而PE⊥OB,
∴OB为⊙P的切线;
故⊙P与OB位置关系是相切;
(2)①存在
∵PA=PB,
∴点P为∠AOB的平分线或反向延长线与⊙O的交点,
如图2,
当P点在优弧AB上时, 设⊙Q的半径为![]() ,
,
若⊙Q与⊙O内切,可得![]() ,解得
,解得![]() ,
,
若⊙Q与⊙O外切,可得![]() , 解得
, 解得![]() ,
,
当P点在劣弧AB上时,
同理可得:x=![]() ,x=
,x=![]() ,
,
综上所述,存在⊙Q,半径可以为![]() ,4 ,
,4 ,![]() ,
,![]() ;
;
②存在.作QH⊥PB于H,如图3,
∵PA⊥PB,
∴∠APB=90°,
∵⊙Q与射线PA.PB相切,
∴PQ平分∠APB,
∴∠QPH=45°,
∴△QHP为等腰直角三角形,
∴QH=PH,
在Rt△POA中,∠AOP=60°,OA=2,
∴OP=1,
设⊙Q的半径为r,即PH=QH=r,则OH=PH﹣OP=r﹣1,
在Rt△OQH中,OQ2=OH2+QH2=(r﹣1)2+r2,
若⊙Q与⊙O内切时,OQ=2﹣r,则(2﹣r)2=(r﹣1)2+r2,解得r1=1,r2=﹣3(舍去);
若⊙Q与⊙O外切时,OQ=2+r,则(2+r)2=(r﹣1)2+r2,解得r1=![]() ,r2=
,r2=![]() (舍去);
(舍去);
综上所述,存在⊙Q,其半径可以为1,![]() .
.
 .
.

 目标测试系列答案
目标测试系列答案【题目】一个金属棒在不同温度下,其长度也不同,其变化情况如下表:
温度/℃ | … | -5 | 0 | 5 | 10 | 15 | … |
长度/ | … | 13.9 | 13.95 | 14 | 14.05 | 14.1 | … |
(1)上述两个变量中,自变量是 ;
(2)设自变量为![]() ,因变量为
,因变量为![]() ,求出
,求出![]() 关于
关于![]() 的解析式;
的解析式;
(3)当温度为30℃时,求金属棒的长度;
(4)若某天金属棒的长度是14.18![]() ,则当天的气温约是多少℃?
,则当天的气温约是多少℃?