Question

【题目】如图①，△ABC中， BD平分∠ABC，且与△ABC的外角∠ACE的角平分线交于点D．

（1）若，，求∠D的度数；

（2）若把∠A截去，得到四边形MNCB，如图②，猜想∠D、∠M、∠N的关系，并说明理由．

Answer 1

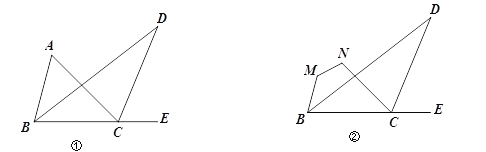
【答案】（1）(2) 或写成

【解析】(1).根据角平分线的定义可得∠DBC=37.5°，根据邻补角定义以及角平分线定义求得∠DCA的度数为67.5°，最后根据三角形内角和定理即可求得∠D的度数；(2).由四边形内角和与角平分线性质即可求解.

本题解析： (1)∵BD平分∠ABC，

∴∠CBD=∠ABC=×75°=37.5°，

∵CD平分△ABC的外角，

∴∠DCA= (180°-∠ACB)= (180°-45°)=67.5°，

∴∠D=180°-∠DBC-∠DCB=180°-37.5°-67.5°-45°=30°；

(2) ∵∠M+∠N+∠CBM+∠NCB=360°,

∴∠D=180°-∠CBM-∠NCB-∠NCE=180°-(360°-∠NCB-∠M-∠N)- ∠NCB-∠NCE=180°-180°+∠NCB+∠M+∠N-∠NCB-∠NCE=∠M+∠N-∠NCB-∠NCE=,或写成.