题目内容
已知二次函数y=ax2+bx+c,一次函数y=k(x-1)-| k2 | 4 |
分析:根据题意由y=ax2+bx+c①,y=k(x-1)-
②,组成的方程组只有一组解,消去y,整理得,ax2+(b-k)x+c+k+
=0,则△=(b-k)2-4a(c+k+
)=0,整理得到(1-a)k2-2(2a+b)k+b2-4ac=0,由于对于任意的实数k都成立,所以有1-a=0,2a+b=0,b2-4ac=0,求出a,b,c即可.
| k2 |
| 4 |
| k2 |
| 4 |
| k2 |
| 4 |
解答:解:根据题意得,
y=ax2+bx+c①,
y=k(x-1)-
②,
解由①②组成的方程组,消去y,整理得,ax2+(b-k)x+c+k+
=0,
∵它们的图象对于任意的实数k都只有一个公共点,则方程组只有一组解,
∴x有两相等的值,
即△=(b-k)2-4a(c+k+
)=0,
∴(1-a)k2-2(2a+b)k+b2-4ac=0,
由于对于任意的实数k都成立,所以有1-a=0,2a+b=0,b2-4ac=0,
∴a=1,b=-2,c=1,
所以二次函数的解析式为y=x2-2x+1.
故答案为:y=x2-2x+1.
y=ax2+bx+c①,
y=k(x-1)-
| k2 |
| 4 |
解由①②组成的方程组,消去y,整理得,ax2+(b-k)x+c+k+
| k2 |
| 4 |
∵它们的图象对于任意的实数k都只有一个公共点,则方程组只有一组解,
∴x有两相等的值,
即△=(b-k)2-4a(c+k+
| k2 |
| 4 |
∴(1-a)k2-2(2a+b)k+b2-4ac=0,
由于对于任意的实数k都成立,所以有1-a=0,2a+b=0,b2-4ac=0,
∴a=1,b=-2,c=1,
所以二次函数的解析式为y=x2-2x+1.
故答案为:y=x2-2x+1.
点评:本题考查了用待定系数法求抛物线的解析式.二次函数的一般式:y=ax2+bx+c(a≠0);也考查了利用方程组的解的情况确定函数图象交点的问题,而方程组的解的情况转化为一元二次方程根的情况.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
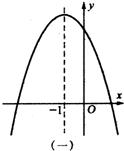 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
