题目内容
 如图,两个等圆⊙O1和⊙O2互过圆心,且交于A、B两点,点P是⊙O2上任意一点(不与A、B重合),则∠APB的度数为
如图,两个等圆⊙O1和⊙O2互过圆心,且交于A、B两点,点P是⊙O2上任意一点(不与A、B重合),则∠APB的度数为
- A.60°或120°
- B.30°或150°
- C.60°
- D.30°
A
分析:根据两圆的半径相等,且每一个圆都经过另一个圆的圆心,根据两圆半径相等,可得△AO1O2为等边三角形,从而得到∠AO2B=120°,即可求出∠APB的度数,再利用P点也可以在劣弧AB上,进而得出∠APB的另一个度数.
解答: 解:连接O1A,O2A,O1B,O2B,O1O2,
解:连接O1A,O2A,O1B,O2B,O1O2,
∵⊙O1与⊙O2为等圆,
∴O1A=O2A=O1B=O2B=O1O2,
∴△AO1O2为等边三角形,
∴∠AO2B=120°,
∴∠APB=60°,
当P在劣弧AB上时,同理可得出:∠APB的度数为120°,
故∠APB的度数为60°或120°.
故选:A.
点评:此题主要考查了相交两圆的性质以及等边三角形的性质和圆周角定理,注意分类讨论思想的应用.
分析:根据两圆的半径相等,且每一个圆都经过另一个圆的圆心,根据两圆半径相等,可得△AO1O2为等边三角形,从而得到∠AO2B=120°,即可求出∠APB的度数,再利用P点也可以在劣弧AB上,进而得出∠APB的另一个度数.
解答:
 解:连接O1A,O2A,O1B,O2B,O1O2,
解:连接O1A,O2A,O1B,O2B,O1O2,∵⊙O1与⊙O2为等圆,
∴O1A=O2A=O1B=O2B=O1O2,
∴△AO1O2为等边三角形,
∴∠AO2B=120°,
∴∠APB=60°,
当P在劣弧AB上时,同理可得出:∠APB的度数为120°,
故∠APB的度数为60°或120°.
故选:A.
点评:此题主要考查了相交两圆的性质以及等边三角形的性质和圆周角定理,注意分类讨论思想的应用.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
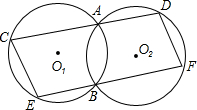 于点C,点D,经过点B的直线与两圆分别交于点E,点F.若CD∥EF,求证:
于点C,点D,经过点B的直线与两圆分别交于点E,点F.若CD∥EF,求证:
 (2013•桐乡市一模)如图,两个等圆⊙O1和⊙O2相交于点A、B,点C在⊙O2上,已知∠AO1B=92°,则∠ACB等于
(2013•桐乡市一模)如图,两个等圆⊙O1和⊙O2相交于点A、B,点C在⊙O2上,已知∠AO1B=92°,则∠ACB等于 .
.
 .
.
