Question

【题目】如图，是的直径，为延长线上的一点，交于点，且．

求证：是的切线；

请直接写出图中某条线段之间的等量关系式，只要写出个．（添加的辅助线不能用）

Answer 1

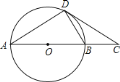
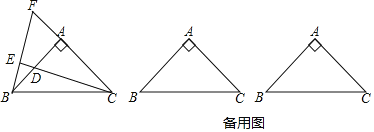
【答案】（1）连结．

是直径，．

，，是等边三角形

而，，

，

即，故是⊙O的切线．

（2）OA=OB=BC=BD

【解析】

（1）连接OD，由AB为圆O的直径，根据直径所对的圆周角为直角得到∠ADB为直角，再由∠A为30°，利用三角形的内角和定理求出∠OBD为60°，再由OD=OB，得到三角形OBD为等边三角形，根据等边三角形的性质得到内角∠ODB为60°，又∠OBD为三角形BDC的外角，利用外角的性质得到∠BDC=∠OBD-∠C，求出∠BDC为30°，进而确定出∠ODC为直角，即DC垂直于OD，可得出CD为圆O的切线，得证；

（2）由O为AB的中点得到OA=OB，再由三角形ODB为等边三角形可得出DB=OB，在直角三角形OCD中，根据30°角所对的直角边等于斜边的一半得出OD为OC的一半，即OB为OC的一半，即B为OC中点，可得出BC=OB，即可得到OA=OB=BC=BD，找出其中的三条线段相等即可．