Question

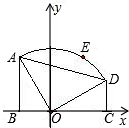如图，直角梯形ABCD中，AB∥DC，AB=

3

，CD=1，以BC上一点O为圆心的圆经过A、D两点，且∠AOD=90°，E是弧AD上一点，且弧DE是弧AD的三分之一；若以BC所在直线为x轴，以过O点且垂直于BC的直线为y轴，则经过E点的反比例函数解析式为

 

．

Answer 1

分析：先通过各角之间的关系，证明△ABO≌△ODC，再求出圆的半径OD和∠EOC，则可求得E点的坐标为E（

3

，1）．
代入解析式y=

k

x

中，即可求得反比例函数的解析式为y=

3

x

．

解答：解：∵∠AOD=90°，
∴∠OAD+∠ODA=90°．
∴∠BAO+∠ODC=90°，
且ABCD是直角梯形，
∠ABC=∠DOC=90°．
∴∠BAO+∠AOB=90°，∠ODC+∠DOC=90°，
∴∠AOB=∠ODC．
又∵以O为圆心的圆经过A、D两点，∴OA=OD，
∴△ABO≌△OCD．
∴AB=OC=

3

．
根据勾股定理，半径OD=

OC2+CD2

=2．
又因为弧DE是弧AD的三分之一，
∴∠EOD=30°，tan∠DOC=

3

3

，
∴∠DOC=30°，∠EOC=60°．
设E点坐标为E（x，y），
则x=OEcos60°=

3

，y=OEsin60°=1，
∴E（

3

，1）．代入y=

k

x

中，得k=

3

，
∴经过E点的反比例函数解析式为y=

3

x

．

点评：解答本题关键是要证△ABO≌△ODC，这就要明确各角之间的关系，同学们要注意观察图象，充分利用每一个已知条件．