Question

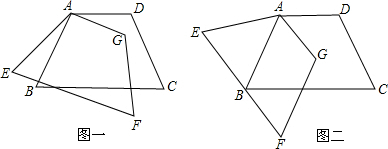
已知：梯形ABCD中，AD∥BC，∠ABC=60°且BC=8，梯形ABCD绕点A顺时针旋转a度后得到梯形AEFG，a为锐角．
（1）如图一，旋转过程中，若线段AB与线段EF始终有交点，求a的范围；
（2）如图二，若B点落在线段EF上，小刚同学用三角板量得F、G和D三点在同一条直线上，由此，他得到四边形ABFG是平行四边形，你能证明吗？请写出理由；
（3）小刚最后又发现中的平行四边形ABFG是菱形，请求出梯形ABCD的面积．

Answer 1

（1）梯形ABCD绕点A顺时针旋转a度后得到梯形AEFG，a为锐角，旋转过程中，当线段AB与线段EF的交点与B点重合，即B点落在线段EF上之前，此时AB=AE，∠E=∠ABC=60°，
∴△AEB为等边三角形，
∴∠EAB=60°，
∴线段AB与线段EF始终有交点，a的范围为0°≤α≤60°；

（2）四边形ABFG是平行四边形．理由如下：
连DG，如图，
∵B点落在线段EF上，F、G和D三点在同一条直线上，
而△ABE为等边三角形，
∴∠EAB=60°，
∴∠BAG=120°-60°=60°，
而AG=AD，
∴△AGD为等边三角形，
∴∠1=60°，
∴∠2=∠1=60°，
∴∠2=∠ABC=60°，
∴GF∥AB，
而AG∥BF，
∴四边形ABFG是平行四边形；

（3）过A作AM⊥EF于M点，
∵平行四边形ABFG是菱形，
∴AG=AB=BF=BE，
而BC=8，
∴AG=4，EF=8，AM=AB•sin60°=

3

2

AB=2

3

，
∴梯形ABCD的面积=梯形AEFG的面积=

1

2

×（4+8）×2

3

=12

3

．