题目内容

7．若|x|=$\sqrt{10}$，则x=$±\sqrt{10}$，-$\sqrt{x}$+5的最大值是5．

分析 由绝对值的性质、二次根式的非负性解答即可．

解答 解：∵|x|=$\sqrt{10}$，
∴x=±$\sqrt{10}$．
∵$\sqrt{x}$≥0，
∴-$\sqrt{x}$≤0．
∴-$\sqrt{x}$+5≤5．
∴-$\sqrt{x}$+5的最大值是5．
故答案为：$±\sqrt{10}$；5．

点评 本题主要考查的是二次根式的定义，由二次根式的非负性得到-$\sqrt{x}$+5≤5是解题的关键．

练习册系列答案
相关题目
17．下列说法中，正确的是（　　）
A．$\frac{1}{27}$的立方根是±$\frac{1}{3}$
B．立方根等于它本身的数是1
C．负数没有立方根
D．互为相反数的两个数的立方根也互为相反数
18．计算：${（{\sqrt{3}-\sqrt{2}}）^2}-\sqrt{3}（{\sqrt{2}-\sqrt{3}}）$．
15．下列说法正确的是（　　）
A．一次函数的图象一定是一条直线
B．直线一定是一次函数的图象
C．一次函数的图象一定经过平面直角坐标系中的三个象限
D．以上说法都不正确
2．（1）在解方程$\frac{（x-2）（2x-3）}{（x-2）（3x+1）}$=1时，能否把方程的左边化简成$\frac{（2x-3）}{（3x+1）}$=1来解？为什么？
（2）在解方程$\frac{x}{2x-3}$=$\frac{2x}{3x-1}$时，能否把方程两边的x约去，化简成$\frac{1}{2x-3}$=$\frac{2}{3x-1}$来解？为什么？
12．计算：2÷$\sqrt{2}$×$\frac{1}{\sqrt{2}}$=1．x÷$\sqrt{x}$×$\frac{1}{\sqrt{x}}$=1．
19．计算：
（1）$\sqrt{24}$$+\sqrt{0.5}$$-（\sqrt{\frac{1}{8}}+\sqrt{6}）$
（2）3$\sqrt{2}$$-2\sqrt{12}-4\sqrt{\frac{1}{8}}$$+3\sqrt{48}$
（3）$\frac{2}{3}\sqrt{9x}$+6$\sqrt{\frac{x}{4}}$-2x$\sqrt{\frac{1}{x}}$
（4）$\sqrt{{a}^{2}b}$$+a\sqrt{\frac{b}{a}}$$-b\sqrt{\frac{a}{b}}$$-\sqrt{a{b}^{2}}$．
16．化简．
（1）$\sqrt{1\frac{15}{49}}$
（2）$\sqrt{\frac{7}{100}}$
（3）$\sqrt{\frac{25{a}^{4}}{9{b}^{2}}}$（a＞0）
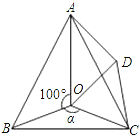4．如图，点O是等边△ABC内一点，∠AOB=100°，∠BOC=α，D是△ABC外一点，且△BOC≌△ADC，连接OD．
（1）△COD是什么三角形？说明理由；
（2）若AO=n2+1，AD=n2-1，OD=2n（n为大于1的整数），求α的度数．
（3）当α为多少度时，△AOD是等腰三角形？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网