题目内容
有两个3×3的正方形网格，网格中每个小正方形的边长均为1．请在图①、图②中各画出一个面积为2，且形状不同的四边形．要求：顶点均在网格的格点上，其中一个是轴对称图形但不是中心对称图形，另一个是中心对称图形但不是轴对称图形．分析：是轴对称但不是中心对称的情况可以选择等腰梯形，是中心对称但不是轴对称的图形可以选择平行四边形．
解答：解：涉及图案如下：
点评：此题考查了在正方形组成的网格中画一定面积的轴对称四边形，对于此类题目要熟悉掌握几种常见的轴对称图形，然后结合题意要求的面积进行设计作图．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
相关题目
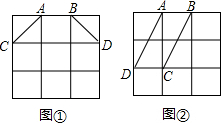
24、如图，在由边长为1的小正方形组成的方格纸中，有两个全等的三角形，即△A1B1C1和△A2B2C2．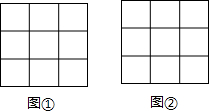
有两个3×3的正方形网格，网格中每个小正方形的边长均为1．请在图①、图②中各画出一个面积为2，且形状不同的四边形．要求：顶点均在网格的格点上，其中一个是轴对称图形但不是中心对称图形，另一个是中心对称图形但不是轴对称图形．