题目内容
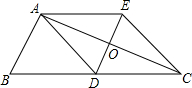 (2012•建宁县质检)如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.
(2012•建宁县质检)如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.(1)求证:AD=EC;
(2)当∠BAC=90°时,求证:四边形ADCE是菱形;
(3)在(2)的条件下,若AB=AO,且OD=a,求菱形ADCE的周长.
分析:(1)首先证明四边形ABDE是平行四边形,可得AE=BD,再根据DC=DB可得AE=DC,进而证出四边形ADCE是平行四边形,可得AD=EC;
(2)当∠BAC=90°时,可证出AD=DC,再根据有一组邻边相等的平行四边形是菱形可得四边形ADCE是菱形;
(3)根据菱形的性质计算出AO=DE=2DO=2a,再根据勾股定理计算出AD的长,进而得到菱形ADCE的周长.
(2)当∠BAC=90°时,可证出AD=DC,再根据有一组邻边相等的平行四边形是菱形可得四边形ADCE是菱形;
(3)根据菱形的性质计算出AO=DE=2DO=2a,再根据勾股定理计算出AD的长,进而得到菱形ADCE的周长.
解答:证明:(1)∵AE∥BC,DE∥AB,
∴四边形ABDE是平行四边形,
∴AE=BD,
∵D是BC中点,
∴DC=DB,
∴AE=DC,AE∥DC,
∴四边形ADCE是平行四边形,
∴AD=EC;
(2)∵当∠BAC=90°时,AD是Rt△ABC斜边上的中线,
∴AD=
BC=CD,
∴四边形ADCE是菱形(有一组邻边相等的平行四边形是菱形);
(3)∵四边形ADCE是菱形,
∴对角线AC⊥DE且O是DE中点,
∵ABDE是平行四边形,
∴AB=DE,
又已知AB=AO
∴AO=DE=2DO=2a,
在Rt△AOD中,可求出AD=
a,
∴菱形ADCE的周长为4
a.
∴四边形ABDE是平行四边形,
∴AE=BD,
∵D是BC中点,
∴DC=DB,
∴AE=DC,AE∥DC,
∴四边形ADCE是平行四边形,
∴AD=EC;
(2)∵当∠BAC=90°时,AD是Rt△ABC斜边上的中线,
∴AD=
| 1 |
| 2 |
∴四边形ADCE是菱形(有一组邻边相等的平行四边形是菱形);
(3)∵四边形ADCE是菱形,
∴对角线AC⊥DE且O是DE中点,
∵ABDE是平行四边形,

∴AB=DE,
又已知AB=AO
∴AO=DE=2DO=2a,
在Rt△AOD中,可求出AD=
| 5 |
∴菱形ADCE的周长为4
| 5 |
点评:此题主要考查了菱形的判定与性质,关键是掌握菱形的判定方法与性质定理.

练习册系列答案
相关题目

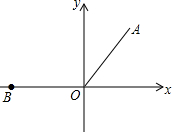 (2012•建宁县质检)如图:在直角坐标系中,线段OA=6cm,OA与y轴的夹角为30°.将线段OA绕原点按逆时针方向旋转到x轴的负半轴上,得到线段OB.
(2012•建宁县质检)如图:在直角坐标系中,线段OA=6cm,OA与y轴的夹角为30°.将线段OA绕原点按逆时针方向旋转到x轴的负半轴上,得到线段OB.