题目内容
已知:如图,在△ABC中,D是AB边上的一点,BD>AD,∠A=∠ACD,(1)若∠A=∠B=30°,BD=
 ,求CB的长;
,求CB的长;(2)过D作∠CDB的平分线DF交CB于F,若线段AC沿着AB方向平移,当点A移到点D时,判断线段AC的中点E能否移到DF上,并说明理由.

【答案】分析:(1)求CB的长,依据已知条件去做;利用外角性质得,∠BDC=∠A+∠ACD=60°,△BCD中,∠BCD=180°-30°-60°=90°,BD=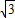 ,CB=BD•cos30°=
,CB=BD•cos30°= ;
;
(2)AC的中点E能移到DF上,则DF> AC根据题中条件证明△BDF∽△BAC,则有
AC根据题中条件证明△BDF∽△BAC,则有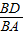 =
=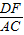 ,BD>AD,
,BD>AD,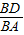 =
=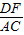 >
> ,DF>
,DF> AC.从而说明所以说E′在线段DF上.
AC.从而说明所以说E′在线段DF上.
解答:解:(1)∵∠A=∠B=30°,
∴∠ACB=120°,
又∠ACD=30°,
∴∠DCB=90°,
∵BD=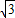 ,
,
∴CB=BD•cos30°= ;
;
(2)AC的中点E能移到DF上.
∵∠CDB=∠A+∠DCA,∠A=∠DCA,
∴∠CDB=2∠A,又DF平分∠CDB,
∴∠CDF=∠FDB=∠A,
∴DF∥AC,
∴△BDF∽△BAC,
∴ =
= ,
,
∵BD>AD,
∴ =
= ,>
,> ,
,
∴DF> AC,
AC,
过E作EE′∥AD交DF于E′,
则四边形AEE′D为平行四边形,
则DE′=DE,
由于DF> AC=AE=DE′,
AC=AE=DE′,
所以说E′在线段DF上.
点评:考查相似三角形的判定,解直角三角形,平行四边形的性质.
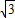 ,CB=BD•cos30°=
,CB=BD•cos30°= ;
;(2)AC的中点E能移到DF上,则DF>
 AC根据题中条件证明△BDF∽△BAC,则有
AC根据题中条件证明△BDF∽△BAC,则有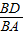 =
=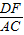 ,BD>AD,
,BD>AD,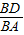 =
=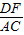 >
> ,DF>
,DF> AC.从而说明所以说E′在线段DF上.
AC.从而说明所以说E′在线段DF上.解答:解:(1)∵∠A=∠B=30°,
∴∠ACB=120°,
又∠ACD=30°,
∴∠DCB=90°,
∵BD=
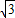 ,
,∴CB=BD•cos30°=
 ;
;(2)AC的中点E能移到DF上.
∵∠CDB=∠A+∠DCA,∠A=∠DCA,
∴∠CDB=2∠A,又DF平分∠CDB,
∴∠CDF=∠FDB=∠A,
∴DF∥AC,
∴△BDF∽△BAC,
∴
 =
= ,
,∵BD>AD,
∴
 =
= ,>
,> ,
,∴DF>
 AC,
AC,过E作EE′∥AD交DF于E′,
则四边形AEE′D为平行四边形,
则DE′=DE,
由于DF>
 AC=AE=DE′,
AC=AE=DE′,所以说E′在线段DF上.
点评:考查相似三角形的判定,解直角三角形,平行四边形的性质.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
34、已知:如图,在AB、AC上各取一点,E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2, (2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(2013•启东市一模)已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. 已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E.
已知:如图,在△ABC中,∠C=120°,边AC的垂直平分线DE与AC、AB分别交于点D和点E. 已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,
已知:如图,在AB、AC上各取一点E、D,使AE=AD,连接BD,CE,BD与CE交于O,连接AO,∠1=∠2,