题目内容
【题目】在正方形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,过点
,过点![]() ,
,![]() 作
作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
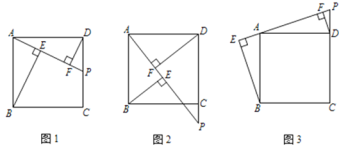
,![]() ,如图1.
,如图1.
(1)请探究![]() ,
,![]() ,
,![]() 这三条线段有怎样的数量关系?请说明理由;
这三条线段有怎样的数量关系?请说明理由;
(2)若点![]() 在
在![]() 的延长线上,如图2,那么这三条线段的数量关系是 (直接写结果)
的延长线上,如图2,那么这三条线段的数量关系是 (直接写结果)
(3)若点![]() 在
在![]() 的延长线上,如图3,那么这三条线段的数量关系是 (直接写结果)
的延长线上,如图3,那么这三条线段的数量关系是 (直接写结果)
【答案】(1)BE=DF+EF,理由见解析; (2) DF=BE+EF;(3) EF=DF+BE.
【解析】
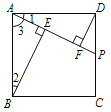
(1)如下图,由已知条件易得∠1=∠2,∠AEB=∠DFA=90°,这样结合AB=AD即可证得△ABE≌△DAF,由此可得BE=AF,AE=DF,结合AF=AE+EF即可得到BE=DF+EF;
(2)和(1)同理可证得△ABE≌△DAF,由此可得BE=AF,AE=DF,结合AF=AE-EF即可得到BE=DF-EF;
(3)和(1)同理可证得△ABE≌△DAF,由此可得BE=AF,AE=DF,结合AF=EF-AE即可得到BE=EF-DF.
(1) ![]() .理由如下:
.理由如下:
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵在![]() 和
和![]() 中,
中,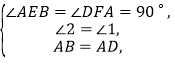
∴△ABE≌△DAF(AAS),
∴![]() ,
,![]() ,
,
∴![]() .
.
(2)如图2,和(1)同理可得△ABE≌△DAF,
∴BE=AF,AE=DF,
又∵AF=AE-EF,
∴BE=DF-EF;
(3)如图3,和(1)同理可证得△ABE≌△DAF,
∴BE=AF,AE=DF,
又∵AF=EF-AE,
∴BE=EF-DF.

练习册系列答案
相关题目