题目内容
 如图,直线y=
如图,直线y= x与双曲线y=
x与双曲线y= (x>0)交于点A,将直线y=
(x>0)交于点A,将直线y= x向下平移个6单位后,与双曲线y=
x向下平移个6单位后,与双曲线y= (x>0)交于点B,与x轴交于点C,则C点的坐标为________;若
(x>0)交于点B,与x轴交于点C,则C点的坐标为________;若 =2,则k=________.
=2,则k=________.
( ,0) 12
,0) 12
分析:根据题意得到直线BC的解析式,令y=0,得到点C的坐标;根据直线AO和直线BC的解析式与双曲线y= 联立求得A,B的坐标,再由已知条件
联立求得A,B的坐标,再由已知条件 =2,从而求出k值.
=2,从而求出k值.
解答: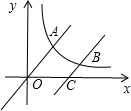 解:∵将直线y=
解:∵将直线y= x向下平移个6单位后得到直线BC,
x向下平移个6单位后得到直线BC,
∴直线BC解析式为:y= x-6,
x-6,
令y=0,得 x-6=0,
x-6=0,
∴C点坐标为( ,0);
,0);
∵直线y= x与双曲线y=
x与双曲线y= (x>0)交于点A,
(x>0)交于点A,
∴A(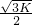 ,
,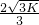 ),
),
又∵直线y= x-6与双曲线y=
x-6与双曲线y= (x>0)交于点B,且
(x>0)交于点B,且 =2,
=2,
∴B( +
+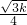 ,
,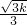 ),将B的坐标代入y=
),将B的坐标代入y= 中,得
中,得
( +
+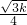 )
)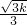 =k,
=k,
解得k=12.
故答案为:( ,0),12.
,0),12.
点评:此题考查一次函数与反比例函数的性质,联立方程求出点的坐标,同时还考查学生的计算能力.
 ,0) 12
,0) 12分析:根据题意得到直线BC的解析式,令y=0,得到点C的坐标;根据直线AO和直线BC的解析式与双曲线y=
 联立求得A,B的坐标,再由已知条件
联立求得A,B的坐标,再由已知条件 =2,从而求出k值.
=2,从而求出k值.解答:
 解:∵将直线y=
解:∵将直线y= x向下平移个6单位后得到直线BC,
x向下平移个6单位后得到直线BC,∴直线BC解析式为:y=
 x-6,
x-6,令y=0,得
 x-6=0,
x-6=0,∴C点坐标为(
 ,0);
,0);∵直线y=
 x与双曲线y=
x与双曲线y= (x>0)交于点A,
(x>0)交于点A,∴A(
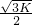 ,
,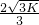 ),
),又∵直线y=
 x-6与双曲线y=
x-6与双曲线y= (x>0)交于点B,且
(x>0)交于点B,且 =2,
=2,∴B(
 +
+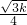 ,
,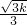 ),将B的坐标代入y=
),将B的坐标代入y= 中,得
中,得(
 +
+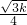 )
) =k,
=k,解得k=12.
故答案为:(
 ,0),12.
,0),12.点评:此题考查一次函数与反比例函数的性质,联立方程求出点的坐标,同时还考查学生的计算能力.

练习册系列答案
相关题目
 如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=
如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于点O,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=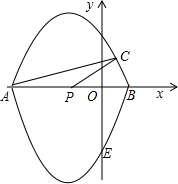 点,且P(-1,0),C(
点,且P(-1,0),C(


