题目内容
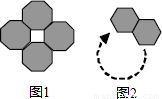
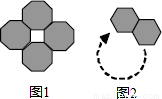
 用4个全等的正八边形进行拼接,使相邻的两个正八边形有一条公共边,围成一圈后中间形成一个正方形,如图1.用n个全等的正六边形按这种方式拼接,如图2,若围成一圈后中间也形成一个正多边形,则n的值为( )
用4个全等的正八边形进行拼接,使相邻的两个正八边形有一条公共边,围成一圈后中间形成一个正方形,如图1.用n个全等的正六边形按这种方式拼接,如图2,若围成一圈后中间也形成一个正多边形,则n的值为( )分析:首先求得正六边形围成的多边形的内角的度数,然后根据多边形的内角和定理即可求得n的值.
解答:解:正六边形的内角度数是:
=120°,
则正六边形围成的多边形的内角的度数是:360-2×120=120°,
根据题意得:180(n-2)=120n,
解得:n=6.
故选B.
| 180(6-2) |
| 6 |
则正六边形围成的多边形的内角的度数是:360-2×120=120°,
根据题意得:180(n-2)=120n,
解得:n=6.
故选B.
点评:本题考查了多边形的内角和定理,正确理解定理,求得围成的多边形的内角的度数是关键.

练习册系列答案
相关题目