题目内容
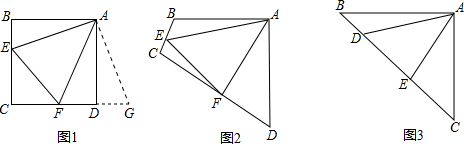
△ABC中，∠BAC=30°，把△ABC按如图方法折叠，∠DEF=36°，则原△ABC的∠ABC=
- A.60°
- B.63°
- C.64°
- D.65°
B
分析：利用示意图得出∠1=∠2=∠3，∠4=∠5，进而利用三角形外角的性质得出即可．
解答：
解：∵把△ABC按如图方法折叠，
∴∠1=∠2=∠3，∠4=∠5，
∵∠DEF=36°，
∴∠4=∠5=
=72°，
∵∠1+∠2+30°=72°，
∴2∠1=42°，
∴∠1=21°，
则原△ABC的∠ABC=21°×3=63°．
故选：B．
点评：此题主要考查了翻折变换的性质以及三角形外角的性质，根据已知得出∠5的度数是解题关键．
分析：利用示意图得出∠1=∠2=∠3，∠4=∠5，进而利用三角形外角的性质得出即可．
解答：
解：∵把△ABC按如图方法折叠，∴∠1=∠2=∠3，∠4=∠5，
∵∠DEF=36°，
∴∠4=∠5=
=72°，∵∠1+∠2+30°=72°，
∴2∠1=42°，
∴∠1=21°，
则原△ABC的∠ABC=21°×3=63°．
故选：B．
点评：此题主要考查了翻折变换的性质以及三角形外角的性质，根据已知得出∠5的度数是解题关键．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
18、如图，在△ABC中，∠BAC=60°，BD、CE分别是边AC，AB上的高，BD、CE相交于点O，则∠BOC的度数是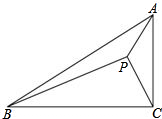
如图，△ABC中，∠BAC=60°，AB=2AC．点P在△ABC内，且PA=
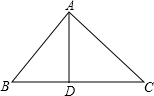如图，在△ABC中，∠BAC=90°，AB=AC=a，AD是△ABC的高，则AD的长为
93、如图所示，在△ABC中，∠BAC=90°，AD⊥BC于D，BF平分∠ABC，那么△AEF是等腰三角形吗？