题目内容
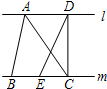 如图,l∥m,BE=EC,S△ABC=10,那么S△DEC=________.
如图,l∥m,BE=EC,S△ABC=10,那么S△DEC=________.
5
分析:由已知l∥m,设l和m的距离为h,则△ABC和△DEC的面积为: BC•h和
BC•h和 EC•h,又由BE=EC,得BC=2EC,所以
EC•h,又由BE=EC,得BC=2EC,所以 ×2EC•h=10,得
×2EC•h=10,得 EC•h=5,从而求出S△DEC.
EC•h=5,从而求出S△DEC.
解答:已知l∥m,和如图所示,设l和m的距离为h,
则S△ABC= BC•h,S△DEC=
BC•h,S△DEC= EC•h,
EC•h,
又BE=EC,∴BC=2EC,
∴所 ×2EC•h=10,
×2EC•h=10,
得 EC•h=5,
EC•h=5,
即S△DEC=5,
故答案为:5.
点评:此题考查的知识点是三角形的面积及平行线之间的距离,关键是由平行线之间的距离得两三角形的高相等结合已知BE=EC求出三角形DEC的面积.
分析:由已知l∥m,设l和m的距离为h,则△ABC和△DEC的面积为:
 BC•h和
BC•h和 EC•h,又由BE=EC,得BC=2EC,所以
EC•h,又由BE=EC,得BC=2EC,所以 ×2EC•h=10,得
×2EC•h=10,得 EC•h=5,从而求出S△DEC.
EC•h=5,从而求出S△DEC.解答:已知l∥m,和如图所示,设l和m的距离为h,
则S△ABC=
 BC•h,S△DEC=
BC•h,S△DEC= EC•h,
EC•h,又BE=EC,∴BC=2EC,
∴所
 ×2EC•h=10,
×2EC•h=10,得
 EC•h=5,
EC•h=5,即S△DEC=5,
故答案为:5.
点评:此题考查的知识点是三角形的面积及平行线之间的距离,关键是由平行线之间的距离得两三角形的高相等结合已知BE=EC求出三角形DEC的面积.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
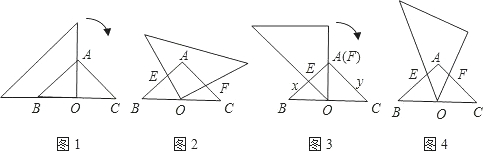 形?若能,直接写出△OEF为等腰三角形时x的值;若不能,请说明理由.
形?若能,直接写出△OEF为等腰三角形时x的值;若不能,请说明理由.

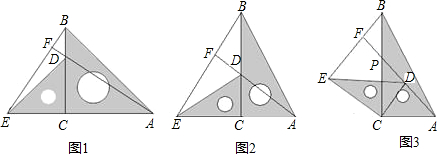
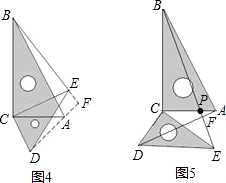
 29、如图,AB=AC,BE=CE 求证:(1)AE平分∠BAC(2)AD垂直平分BC
29、如图,AB=AC,BE=CE 求证:(1)AE平分∠BAC(2)AD垂直平分BC 如图,AB=AC,BE⊥AC于E,CF⊥AB于F,则①△ABE≌△ACF;②△BOF≌△COE;③点O在∠BAC的角平分线上,其中正确的结论是( )
如图,AB=AC,BE⊥AC于E,CF⊥AB于F,则①△ABE≌△ACF;②△BOF≌△COE;③点O在∠BAC的角平分线上,其中正确的结论是( )