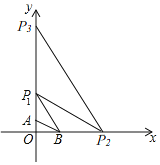Question

【题目】如图，为轴上一点，为的中点，，为反比例函数的图象上两点，且，，若，则________．

Answer 1

【答案】

【解析】

作CE⊥x轴于E点，作DF⊥x轴于F点，如图，根据等腰三角形的性质得OE=BE，BF=AF，由于B点为OA的中点，则OF=3OE，设C（t，），易得B（2t，0），F（3t，0），A（4t，0），再确定D（3t，），然后根据三角形面积公式得到2t+2t=4，然后解方程即可．

作CE⊥x轴于E点，作DF⊥x轴于F点，如图，

∵OC=BC，AD=BD，

∴OE=BE，BF=AF．

∵B点为OA的中点，

∴OF=3OE，

设C（t，），则B（2t，0），F（3t，0），A（4t，0），当x=3t时，y=，则D（3t，）．

∵S△OBC+S△ABD=4，

∴2t+2t=4，

解得：k=3．

故答案为：3．