题目内容
如图,已知射线OM与射线ON互相垂直,A是射线OM上一点,B是射线ON上一点,且OA=OB=1,圆A与直线ON相切,那么当圆B与圆A相切时,圆B的半径等于 .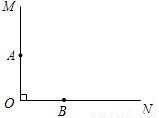
【答案】分析:根据相切两圆的性质,以及利用两圆相外切或相内切分别得出圆B的半径即可.
解答: 解:如图所示:
解:如图所示:
当两圆外切,
∵AO=BO=1,
∴AB= ,
,
∴BD=AB-AD= -1,
-1,
当两圆内切,
∵AB= ,AC=AO=1,
,AC=AO=1,
∴BC=AB+AC= +1,
+1,
故圆B的半径等于: -1或
-1或 +1,
+1,
故答案为: -1或
-1或 +1.
+1.
点评:此题主要考查了相切两圆的性质,根据已知得出两圆存在两种位置关系是解题关键.
解答:
 解:如图所示:
解:如图所示:当两圆外切,
∵AO=BO=1,
∴AB=
 ,
,∴BD=AB-AD=
 -1,
-1,当两圆内切,
∵AB=
 ,AC=AO=1,
,AC=AO=1,∴BC=AB+AC=
 +1,
+1,故圆B的半径等于:
 -1或
-1或 +1,
+1,故答案为:
 -1或
-1或 +1.
+1.点评:此题主要考查了相切两圆的性质,根据已知得出两圆存在两种位置关系是解题关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目

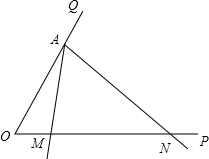 的位置开始,按逆时针方向旋转(∠MAN保持不变)时,M、N两点在射线OP上同时以不同的速度向右平行移动,设OM=x,ON=y(y>x≥0).
的位置开始,按逆时针方向旋转(∠MAN保持不变)时,M、N两点在射线OP上同时以不同的速度向右平行移动,设OM=x,ON=y(y>x≥0).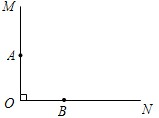 如图,已知射线OM与射线ON互相垂直,A是射线OM上一点,B是射线ON上一点,且OA=OB=1,圆A与直线ON相切,那么当圆B与圆A相切时,圆B的半径等于
如图,已知射线OM与射线ON互相垂直,A是射线OM上一点,B是射线ON上一点,且OA=OB=1,圆A与直线ON相切,那么当圆B与圆A相切时,圆B的半径等于 如图,已知射线OM与射线ON互相垂直,A是射线OM上一点,B是射线ON上一点,且OA=OB=1,圆A与直线ON相切,那么当圆B与圆A相切时,圆B的半径等于________.
如图,已知射线OM与射线ON互相垂直,A是射线OM上一点,B是射线ON上一点,且OA=OB=1,圆A与直线ON相切,那么当圆B与圆A相切时,圆B的半径等于________.