题目内容
(1)计算: +
+ ;
;
(2)计算: ;
;
(3)已知(x+1)2-1=24,求x的值.
(4)已知x是 的整数部分,y是
的整数部分,y是 的小数部分,求(y-
的小数部分,求(y- )-X+1的平方根.
)-X+1的平方根.
解:(1) -
- +(3-
+(3- )0,
)0,
=3-2+1,
=2;
(2) -
-
 +(
+( -π)0+(-
-π)0+(-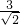 )-1,
)-1,
= -1-
-1- +1-
+1- ,
,
= -1-
-1- +1,
+1,
=0;
(3)由(x+1)2-1=24得(x+1)2=25,
所以,x+1=±5,
所以,x1=4,x2=-6;
(4)∵3< <4,
<4,
∴x=3,y= -3,
-3,
∴(y- )-X+1=(
)-X+1=( -3-
-3- )-3+1=(-3)-2=
)-3+1=(-3)-2= ,
,
∴(y- )-X+1的平方根是±
)-X+1的平方根是±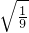 =±
=± .
.
分析:(1)根据立方根的定义,二次根式的运算,任何非0数的0次幂等于1进行计算即可得解;
(2)把第一个算式分母有理化,第二个化为最简二次根式,任何非0数的0次幂等于1,实数的负整数指数次幂等于正整数指数次幂的倒数进行计算即可得解;
(3)先求出(x+1)2的值,再利用直接开平方法求解;
(4)根据无理数的估算求出x、y的值,然后代入代数式求出(y- )-X+1的值,再根据平方根的定义解答.
)-X+1的值,再根据平方根的定义解答.
点评:本题考查的是二次根式的混合运算,零指数幂,负整数指数幂的性质,无理数的大小估算,在进行此类运算时一般先把二次根式化为最简二次根式的形式后再运算.
 -
- +(3-
+(3- )0,
)0,=3-2+1,
=2;
(2)
 -
-
 +(
+( -π)0+(-
-π)0+(-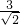 )-1,
)-1,=
 -1-
-1- +1-
+1- ,
,=
 -1-
-1- +1,
+1,=0;
(3)由(x+1)2-1=24得(x+1)2=25,
所以,x+1=±5,
所以,x1=4,x2=-6;
(4)∵3<
 <4,
<4,∴x=3,y=
 -3,
-3,∴(y-
 )-X+1=(
)-X+1=( -3-
-3- )-3+1=(-3)-2=
)-3+1=(-3)-2= ,
,∴(y-
 )-X+1的平方根是±
)-X+1的平方根是±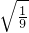 =±
=± .
.分析:(1)根据立方根的定义,二次根式的运算,任何非0数的0次幂等于1进行计算即可得解;
(2)把第一个算式分母有理化,第二个化为最简二次根式,任何非0数的0次幂等于1,实数的负整数指数次幂等于正整数指数次幂的倒数进行计算即可得解;
(3)先求出(x+1)2的值,再利用直接开平方法求解;
(4)根据无理数的估算求出x、y的值,然后代入代数式求出(y-
 )-X+1的值,再根据平方根的定义解答.
)-X+1的值,再根据平方根的定义解答.点评:本题考查的是二次根式的混合运算,零指数幂,负整数指数幂的性质,无理数的大小估算,在进行此类运算时一般先把二次根式化为最简二次根式的形式后再运算.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
