Question

14．如图，将边长为3的正六边形A₁ A₂ A₃ A₄ A₅ A₆在直线l上由图1的位置按顺时针方向向右作无滑动滚动，当A₁第一次滚动到图2位置时，顶点A₁所经过的路径的长为（4+2$\sqrt{3}$）π．

Answer 1

分析 连A₁A₅，A₁A₄，A₁A₃，作A₆C⊥A₁A₅，利用正六边形的性质分别计算出A₁A₄=2a，A₁A₅=A₁A₃=3$\sqrt{3}$，而当A₁第一次滚动到图2位置时，顶点A₁所经过的路径分别是以A₆，A₅，A₄，A₃，A₂为圆心，以3，3$\sqrt{3}$，6，3$\sqrt{3}$，3为半径，圆心角都为60°的五条弧，然后根据弧长公式进行计算即可．

解答 解：连A₁A₅，A₁A₄，A₁A₃，作A₆C⊥A₁A₅，如图，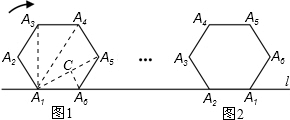

∵六边形A₁A₂A₃A₄A₅A₆为正六边形，
∴A₁A₄=6，∠A₁A₆A₅=120°，
∴∠CA₁A₆=30°，
∴A₆C=$\frac{3}{2}$，A₁C=$\frac{3\sqrt{3}}{2}$，
∴A₁A₅=A₁A₃=3$\sqrt{3}$，
当A₁第一次滚动到图2位置时，顶点A₁所经过的路径分别是以A₆，A₅，A₄，A₃，A₂为圆心，
以3，3$\sqrt{3}$，6，3$\sqrt{3}$，3为半径，圆心角都为60°的五条弧，
∴顶点A₁所经过的路径的长=$\frac{60π×3}{180}$+$\frac{60π×3\sqrt{3}}{180}$+$\frac{60π×6}{180}$+$\frac{60π×3\sqrt{3}}{180}$+$\frac{60π×3}{180}$=（4+2$\sqrt{3}$）π，
故答案为：（4+2$\sqrt{3}$）π．

点评 本题考查了轨迹，弧长公式：l=$\frac{nπr}{180}$，也考查了正六边形的性质以及旋转的性质，难度一般．