题目内容
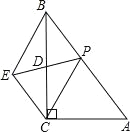
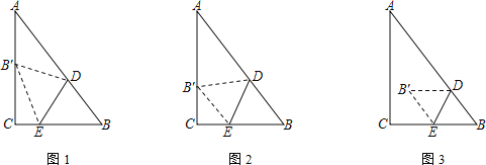
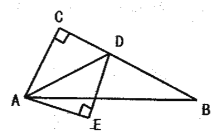
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的动点,连接
边上的动点,连接![]() ,以
,以![]() 为斜边在
为斜边在![]() 的下方作等腰直角三角形
的下方作等腰直角三角形![]() .
.
(1)填空:![]() 的面积等于 ;
的面积等于 ;
(2)连接![]() ,求证:
,求证:![]() 是
是![]() 的平分线;
的平分线;
(3)点![]() 在
在![]() 边上,且
边上,且![]() , 当
, 当![]() 从点
从点![]() 出发运动至点
出发运动至点![]() 停止时,求点
停止时,求点![]() 相应的运动路程.
相应的运动路程.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]()
【解析】
(1)根据直角三角形的面积计算公式直接计算可得;
(2)如图所示作出辅助线,证明△AEM≌△DEN(AAS),得到ME=NE,即可利用角平分线的判定证明;
(3)由(2)可知点E在∠ACB的平分线上,当点D向点B运动时,点E的路径为一条直线,再根据全等三角形的性质得出CN=![]() ,根据CD的长度计算出CE的长度即可.
,根据CD的长度计算出CE的长度即可.
解:(1)![]()
∴![]() ,
,
故答案为:![]()
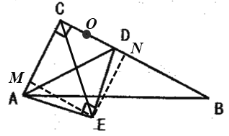
(2)连接CE,过点E作EM⊥AC于点M,作EN⊥BC于点N,
∴∠EMA=∠END=90°,
又∵∠ACB=90°,
∴∠MEN=90°,
∴∠MED+∠DEN=90°,
∵△ADE是等腰直角三角形
∴∠AED=90°,AE=DE
∴∠AEM+∠MED=90°,
∴∠AEM=∠DEN
∴在△AEM与△DEN中,
∠EMA=∠END=90°,∠AEM=∠DEN,AE=DE
∴△AEM≌△DEN(AAS)
∴ME=NE
∴点E在∠ACB的平分线上,
即![]() 是
是![]() 的平分线
的平分线

(3)由(2)可知,点E在∠ACB的平分线上,
∴当点D向点B运动时,点E的路径为一条直线,
∵△AEM≌△DEN
∴AM=DN,
即AC-CM=CN-CD
在Rt△CME与Rt△CNE中,CE=CE,ME=NE,
∴Rt△CME≌Rt△CNE(HL)
∴CM=CN
∴CN=![]() ,
,
又∵∠MCE=∠NCE=45°,∠CME=90°,
∴CE=![]() ,
,
当AC=3,CD=CO=1时,
CE=![]()
当AC=3,CD=CB=7时,
CE=![]()
∴点E的运动路程为:![]() ,
,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目