题目内容
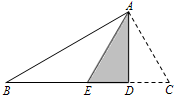
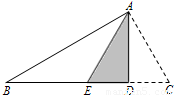
 如图,AD是在Rt△ABC斜边BC上的高,将△ADC沿AD所在直线折叠,点C恰好落在BC的中点处,则∠B等于
如图,AD是在Rt△ABC斜边BC上的高,将△ADC沿AD所在直线折叠,点C恰好落在BC的中点处,则∠B等于
- A.25°
- B.30°
- C.45°
- D.60°
B
分析:先根据图形折叠的性质得出AC=AE,再由直角三角形斜边的中线等于斜边的一半即可得出BE=CE,进而可判断出△AEC是等边三角形,由等边三角形的性质及直角三角形两锐角互补的性质即可得出结论.
解答: 解:△ADC沿AD所在直线折叠,点C恰好落在BC的中点处,则AC=AE,
解:△ADC沿AD所在直线折叠,点C恰好落在BC的中点处,则AC=AE,
∵E为BC中点,△ABC是直角三角形,
∴AE=BE=CE,
∴AC=AE=EC,
∴△AEC是等边三角形.
∴∠C=60°,
∴∠B=30°.
故选B.
点评:本题考查了翻折变换(折叠问题).解题时利用了直角三角形的性质,等边三角形的判定及图形折叠等知识.
分析:先根据图形折叠的性质得出AC=AE,再由直角三角形斜边的中线等于斜边的一半即可得出BE=CE,进而可判断出△AEC是等边三角形,由等边三角形的性质及直角三角形两锐角互补的性质即可得出结论.
解答:
 解:△ADC沿AD所在直线折叠,点C恰好落在BC的中点处,则AC=AE,
解:△ADC沿AD所在直线折叠,点C恰好落在BC的中点处,则AC=AE,∵E为BC中点,△ABC是直角三角形,
∴AE=BE=CE,
∴AC=AE=EC,
∴△AEC是等边三角形.
∴∠C=60°,
∴∠B=30°.
故选B.
点评:本题考查了翻折变换(折叠问题).解题时利用了直角三角形的性质,等边三角形的判定及图形折叠等知识.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2008•海口一模)如图,AD是在Rt△ABC斜边BC上的高,将△ADC沿AD所在直线折叠,点C恰好落在BC的中点处,则∠B等于( )
(2008•海口一模)如图,AD是在Rt△ABC斜边BC上的高,将△ADC沿AD所在直线折叠,点C恰好落在BC的中点处,则∠B等于( )