Question

作图探究：如图，点P是直角坐标系xOy第三象限内一点．
（1）尺规作图：请在图中作出经过O、P两点且圆心在x轴的⊙M；（不写作法，保留作图痕迹）
（2）若点P的坐标为（-4，-2）．
①请求出⊙M的半径；
②填空：若Q是⊙M上的点，且∠PMQ=90°，则点Q的坐标为

 

．

Answer 1

分析：（1）连接OP，作OP的垂直平分线交x轴于M点，以MO我半径作⊙M，即为所求；
（2）①连接PM，作PH⊥x轴，垂足为H，设⊙O的半径为r，则PM=MO=r，MH=4-r，PH=2，在Rt△PHM中，由勾股定理求r即可；
②过M点作PM的垂线，交⊙M于Q₁，Q₂，再过Q₁，Q₂，作x轴的垂线，利用三角形全等求Q点坐标．

解答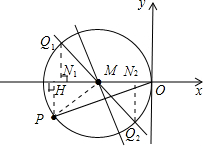：解：（1）⊙M如图所示；

（2）①连接PM，作PH⊥x轴，垂足为H，设⊙O的半径为r，则PM=MO=r，MH=4-r，PH=2，
在Rt△PHM中，PH²+MH²=PM²，
即2²+（4-r）²=r²，
解得r=

5

2

；
②如图，过M点作PM的垂线，交⊙M于Q₁，Q₂，再过Q₁，Q₂，作x轴的垂线，垂足为N₁，N₂，
利用互余关系，PM=Q₁M=Q₂M，
可证Rt△PMH≌Rt△Q₁MN₁≌Rt△Q₂MN₂，
∴PH=MN₁=MN₂=2，MH=Q₁N₁=Q₂N₂=4-r=

3

2

，
∴Q（-

9

2

，

3

2

）或（-

1

2

，-

3

2

）．
故答案为：（-

9

2

，

3

2

）或（-

1

2

，-

3

2

）．

点评：本题考查了垂径定理，勾股定理，尺规作图的知识．关键是将问题转化到直角三角形中，利用勾股定理，全等三角形解题．