题目内容
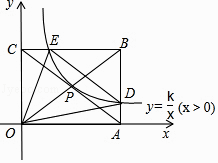
【题目】如图,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在反比例函数
在反比例函数![]() 的第一象限内的图像上,
的第一象限内的图像上,![]() ,
,![]() ,动点
,动点![]() 在
在![]() 轴的上方,且满足
轴的上方,且满足![]() .
.
(1)若点![]() 在这个反比例函数的图像上,求点
在这个反比例函数的图像上,求点![]() 的坐标;
的坐标;
(2)连接![]() 、
、![]() ,求
,求![]() 的最小值;
的最小值;
(3)若点![]() 是平面内一点,使得以
是平面内一点,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形,则请你直接写出满足条件的所有点
为顶点的四边形是菱形,则请你直接写出满足条件的所有点![]() 的坐标.
的坐标.

【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]() 的最小值
的最小值![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 、
、![]() 、
、![]() 、
、![]()
【解析】
(1)根据已知得出点![]() 的坐标为
的坐标为![]() ,从而得出
,从而得出![]() .设点
.设点![]() 的纵坐标为
的纵坐标为![]() ,
,
由![]() ,得出m的值,即可得出P的坐标.
,得出m的值,即可得出P的坐标.
(2)过点![]() 作直线
作直线![]() 轴.由(1)知,点
轴.由(1)知,点![]() 的纵坐标为
的纵坐标为![]() ,从而得出点
,从而得出点![]() 在直线
在直线![]() 上.作点
上.作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,则
,则![]() .连接
.连接![]() 交直线
交直线![]() 于点
于点![]() ,此时
,此时![]() 的值最小,根据勾股定理即可得出结论.
的值最小,根据勾股定理即可得出结论.
(3)画出图形,根据图形直接写出结论即可.
(1)∵四边形![]() 是矩形,
是矩形,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∵点![]() 在反比例函数
在反比例函数![]() 的第一象限内的图像上,
的第一象限内的图像上,
∴![]() ,
,
∴![]() .
.

∴![]() ,
,
设点![]() 的纵坐标为
的纵坐标为![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
当点![]() 在这个反比例函数图像上时,则
在这个反比例函数图像上时,则![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
(2)过点![]() 作直线
作直线![]() 轴.
轴.
由(1)知,点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴点![]() 在直线
在直线![]() 上.
上.
作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,则
,则![]() .
.
连接![]() 交直线
交直线![]() 于点
于点![]() ,此时
,此时![]() 的值最小,
的值最小,
则![]() 的最小值
的最小值![]() .
.
(3)点![]() 的坐标为
的坐标为![]() 、
、![]() 、
、![]() 、
、![]() .
.



练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目