Question

【题目】在△ABC中，∠A、∠B满足，求

（1）∠C的大小；

（2）若AC=12，求BC的长.

Answer 1

【答案】（1）；（2）

【解析】试题分析：（1）由绝对值和偶次方的非负性质和三角函数求出∠A=30°，∠B=45°，再由三角形内角和定理即可求出∠C的度数；

（2）作CD⊥AB于D，由含30°角的直角三角形的性质求出CD=AC=6，证出△BCD是等腰直角三角形，由勾股定理得出BC=CD=6即可．

试题解析：(1)∵|sinA12|+(sinB)2=0，

∴sinA=0，sinB=0，

∴sinA=，sinB=,

∴∠A=30°，∠B=45°，

∴∠C=180°∠A∠B=105°；

(2)作CD⊥AB于D，如图所示，

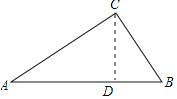
∵AC=12，∠A=30°，

∴CD=AC=6，

∵∠B=45°，

∴△BCD是等腰直角三角形，

∴BD=CD=6，BC=CD=6.