题目内容
(2013•闵行区三模)已知:点G为Rt△ABC的重心,D为斜边AB的中点,如果AC=
,BC=2
,那么线段GD的长等于
.
| 5 |
| 2 |
| ||
| 6 |
| ||
| 6 |
分析:利用勾股定理列式求出斜边AB,再根据直角三角形斜边上的中线等于斜边的一半求出CD,然后三角形的重心到三角形顶点的距离等于到对边中点的距离的2倍求解即可.
解答: 解:∵AC=
解:∵AC=
,BC=2
,
∴斜边AB=
=
=
,
∵D为斜边AB的中点,
∴CD=
AB=
,
∵点G为Rt△ABC的重心,
∴CG=2GD,
∴GD=
CD=
×
=
.
故答案为:
.
 解:∵AC=
解:∵AC=| 5 |
| 2 |
∴斜边AB=
| AC2+BC2 |
|
| 13 |
∵D为斜边AB的中点,
∴CD=
| 1 |
| 2 |
| ||
| 2 |
∵点G为Rt△ABC的重心,
∴CG=2GD,
∴GD=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
故答案为:
| ||
| 6 |
点评:本题考查了三角形的重心,勾股定理,直角三角形斜边上的中线等于斜边的一半的性质,难点在于利用“三角形的重心到三角形顶点的距离等于到对边中点的距离的2倍”,此内容大部分教材已经删去.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
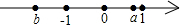 (2013•闵行区三模)已知实数a、b在数轴上的位置如图所示,那么下列等式成立的是( )
(2013•闵行区三模)已知实数a、b在数轴上的位置如图所示,那么下列等式成立的是( )