题目内容
如图,抛物线y=ax2+bx-3与x轴交于两点A(1,0)、B(3,0),与y轴交于点D.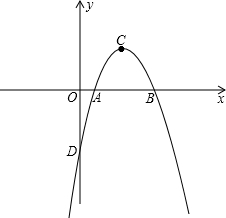
(1)求抛物线的解析式;
(2)在抛物线是否存在一点P,使得△BDP是以BD为斜边的直角三角形,若存在,请求出点P的坐标;若不存在,请说明理由;
(3)在x轴下方的抛物线上是否存在点M,过M作MN⊥x轴于点N,使以A、M、N为顶点的三角形与△BCD相似?若存在,则求出点M的坐标;若不存在,请说明理由.
分析:(1)利用待定系数法求出二次函数解析式即可;
(2)过P作x轴的平行线交Y轴于E点,过B点作X轴的垂线交EP的延长线于F点,利用三角形相似得出P点的坐标;
(3)利用△AMN∽△CDB,当N在A点左边时,当N在A点右边时,当N在A点右边时,当N在A点左边时分别得出即可.
(2)过P作x轴的平行线交Y轴于E点,过B点作X轴的垂线交EP的延长线于F点,利用三角形相似得出P点的坐标;
(3)利用△AMN∽△CDB,当N在A点左边时,当N在A点右边时,当N在A点右边时,当N在A点左边时分别得出即可.
解答:解:(1)∵抛物线y=ax2+bx-3与x轴交于两点A(1,0)、B(3,0),
∴0=a+b-3,0=9a+3b-3,
解得:a=-1,b=4,
∴y=-x2+4x-3;
(2)如图1,过P作x轴的平行线交Y轴于E点,过B点作X轴的垂线交EP的延长线于F点,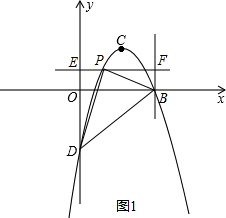
设P(t,-t2+4t-3),当P点在第一象限时,则DE=-t2+4t,PF=3-t,PE=t,BF=-t2+4t-3,
可证△DEP∽△PFB,
=
,
=
,
可求得t=
,
所以P(
,
),
同理,当P点在第四象限时,可求得P(
,
);
(3)如图2,设N(m,0)则M(m,-m2+4m-3),MN=m2-4m+3
若△AMN∽△CDB,
=
=
=3,
当N在A点左边时AN=1-m,
=3,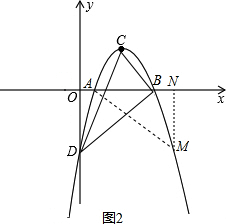
m=0或m=1(舍),所以M(0,-3),
当N在A点右边时AN=m-1,
=3,
m=6或m=1(舍),所以M(6,-15),
若△MAN∽△CDB,
=
=
=3,
当N在A点左边时AN=1-m,
=3,
m=
(舍)或m=1(舍),所以此时M不存在,
当N在A点右边时AN=m-1,
=3,
m=
或m=1(舍),
所以M(
,-
),
综上M1(0,-3)M2(6,-15)M3(
,-
).
∴0=a+b-3,0=9a+3b-3,
解得:a=-1,b=4,
∴y=-x2+4x-3;
(2)如图1,过P作x轴的平行线交Y轴于E点,过B点作X轴的垂线交EP的延长线于F点,

设P(t,-t2+4t-3),当P点在第一象限时,则DE=-t2+4t,PF=3-t,PE=t,BF=-t2+4t-3,
可证△DEP∽△PFB,
| DE |
| PE |
| PF |
| BF |
| -t2+4t |
| t |
| 3-t |
| -t2+4t-3 |
可求得t=
5-
| ||
| 2 |
所以P(
5-
| ||
| 2 |
| ||
| 2 |
同理,当P点在第四象限时,可求得P(
5+
| ||
| 2 |
-
| ||
| 2 |
(3)如图2,设N(m,0)则M(m,-m2+4m-3),MN=m2-4m+3
若△AMN∽△CDB,
| MN |
| AN |
| BD |
| BC |
3
| ||
|
当N在A点左边时AN=1-m,
| m2-4m+3 |
| 1-m |

m=0或m=1(舍),所以M(0,-3),
当N在A点右边时AN=m-1,
| m2-4m+3 |
| m-1 |
m=6或m=1(舍),所以M(6,-15),
若△MAN∽△CDB,
| AN |
| MN |
| BD |
| BC |
3
| ||
|
当N在A点左边时AN=1-m,
| 1-m |
| m2-4m+3 |
m=
| 8 |
| 3 |
当N在A点右边时AN=m-1,
| m-1 |
| m2-4m+3 |
m=
| 10 |
| 3 |
所以M(
| 10 |
| 3 |
| 7 |
| 9 |
综上M1(0,-3)M2(6,-15)M3(
| 10 |
| 3 |
| 7 |
| 9 |
点评:此题主要考查了二次函数的综合应用,(2)(3)小题中,都用到了分类讨论的数学思想,难点在于考虑问题要全面,做到不重不漏.

练习册系列答案
相关题目
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).