��Ŀ����
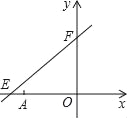
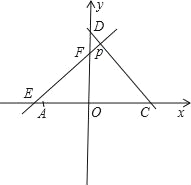
����Ŀ����ͼ��ֱ��y=![]() x+6��x�ᡢy��ֱ��ཻ�ڵ�E��F����A������Ϊ����6��0����P��x��y����ֱ��y=
x+6��x�ᡢy��ֱ��ཻ�ڵ�E��F����A������Ϊ����6��0����P��x��y����ֱ��y=![]() x+6��һ�����㣮
x+6��һ�����㣮
��1���ڵ�P�˶������У���д����OPA�����s��x�ĺ�����ϵʽ��
��2����P�˶���ʲôλ�ã���OPA�����Ϊ![]() �������ʱ��P�����ꣻ
�������ʱ��P�����ꣻ
��3����P��EF�Ĵ��߷ֱ�x�ᡢy����C��D���Ƿ���������ĵ�P��ʹ��COD�ա�FOE�������ڣ�ֱ��д����ʱ��P�����꣨��Ҫ��д�����̣����������ڣ���˵�����ɣ�
���𰸡���1��s=![]() x+18��x����8����s=��
x+18��x����8����s=��![]() x��18��x����8������2������6.5��
x��18��x����8������2������6.5�� ![]() ����9.5����1.125����3������P�㣬ʹ��COD�ա�FOE��P�������ǣ���
����9.5����1.125����3������P�㣬ʹ��COD�ա�FOE��P�������ǣ���![]() ��
�� ![]() ����
����![]() ��
�� ![]() ����
����
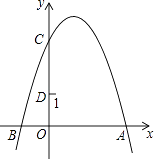
�����������������
��1������֪�����ɵ�OA=6�����P������Ϊ![]() �����P��OA�ľ���Ϊ
�����P��OA�ľ���Ϊ![]() ���ֵ�P�ڵ�һ�������͵���������������ֱ��������S��x��Ĺ�ϵʽ���ɣ�
���ֵ�P�ڵ�һ�������͵���������������ֱ��������S��x��Ĺ�ϵʽ���ɣ�
��2����S=![]() ���루1�������ù�ϵʽ�����x��ֵ������ö�Ӧ�ĵ�P�����ꣻ
���루1�������ù�ϵʽ�����x��ֵ������ö�Ӧ�ĵ�P�����ꣻ
��3����ͼ���ֵ�D��y��������������������������֪�������ۼ��㼴����ö�Ӧ�ĵ�P������.
���������
��1���ߵ�A������Ϊ��-6��0����
��OA=6��
����P��ֱ��![]() ����
����
�������P������Ϊ![]() ��
��
��ֱ��![]() ��x�ύ�ڵ�E����y�ύ�ڵ�F��
��x�ύ�ڵ�E����y�ύ�ڵ�F��
����E��F������ֱ�Ϊ��-8��0���ͣ�0��6����
�൱��P�ڵ�һ��������ʱ����OPA�����S=![]() ��OA��
��OA��![]() =
=![]() ��
��
����P�ڵ�������ʱ����OPA�����S=![]() ��OA��
��OA��![]() =
=![]() ��
��
���P�˶������У���OPA�����s��x�ĺ�����ϵʽ��S=![]() ��S=
��S=![]() ��
��
��2����S=![]() ����S=
����S=![]() ��S=
��S=![]() �ã�
�ã�
![]() ��
��![]() ��
��
����� ![]() ��
��![]() ��
��
����P������Ϊ![]() ��
��![]() ��
��
��3���������P�㣬ʹ��COD�ա�FOE����OD=OE=8��OC=OF=6��
����ͼ������D��y��ĸ�����ʱ����C��x��ĸ����ᣬ
��OD=8��OC=6��
����D��C������ֱ�Ϊ��0��-8���ͣ�-6��0��,
��ֱ��CD�Ľ���ʽΪ��y=kx+b���� ![]() �����
�����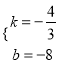 ��
��
��![]() ��
��
��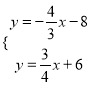 ��ã�
��ã� 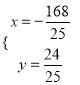 ��
��
����P������Ϊ![]() ��
��
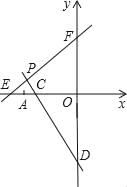
������ͼ��ʾ������D��y��������ʱ����C��x��������ᣬͬ���ɽ�ô�ʱ��P������Ϊ![]() ��
��
��������������P�㣬ʹ��COD�ա�FOE��P��������![]() ��
��![]() ��
��