Question

【题目】如图，已知A、B两点的坐标分别为（2，0）、（0，4），P是△AOB外接圆⊙C上的一点，且∠AOP=45°，则点P的坐标为________．

Answer 1

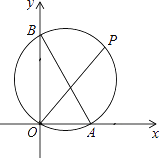
【答案】（3，3）

【解析】

由OA与OB的长，利用勾股定理求出AB的长，根据∠AOP=45°，得到三角形OPE为等腰直角三角形，即P横纵坐标相等，设为P（a，a），由∠AOB为直角，利用直角所对的弦为直径得到AB为直径，Rt△AOB外接圆的圆心为AB中点，求出圆心C坐标，过点C作CF∥OA，过点P作PE⊥OA于E交CF于F，在直角三角形PCF中，利用勾股定理列出关于a的方程，求出方程的解得到a的值，确定出P的坐标即可．

：

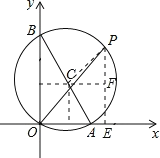∵OB=4，OA=2，

∴AB==2，

∵∠AOP=45°，

∴P点横纵坐标相等,可设为a,即P(a,a)，

∵∠AOB=90°，

∴AB是直径，

∴Rt△AOB外接圆的圆心为AB中点,坐标C(1,2)，

P点在圆上,P点到圆心的距离为圆的半径，

过点C作CF∥OA，过点P作PE⊥OA于E交CF于F，

∴∠CFP=90°，

∴PF=a2,CF=a1,PC=，

∴根据勾股定理得：(a2)2+(a1)2=()2，

解得：a=3，

∴P(3,3)；

故答案为：(3,3).