题目内容
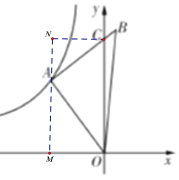
【题目】如图,点![]() 在反比例函数
在反比例函数![]()
![]() 的图象上,连接
的图象上,连接![]() ,作
,作![]() ,且
,且![]() ,线段
,线段![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
过A作AM⊥x轴于M,作CN⊥AM,交MA延长线于N,根据![]() ,△COB的面积
,△COB的面积![]() ,易求得△AOC的面积为
,易求得△AOC的面积为![]() ,进而求得S△AOM+S△ANC=S△AOC=
,进而求得S△AOM+S△ANC=S△AOC=![]() ,通过证得△OAM∽△ACN,得出
,通过证得△OAM∽△ACN,得出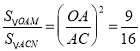 ,即可求得S△OBM=
,即可求得S△OBM=![]() =6,根据反比例函数系数k的几何意义,即可确定k的值.
=6,根据反比例函数系数k的几何意义,即可确定k的值.
解:过A作AM⊥x轴于M,作CN⊥AM,交MA延长线于N,
∵![]() ,△COB的面积
,△COB的面积![]()
∴S△AOC=3S△COB=![]()
∵四边形OMNC是矩形
∴S△AOM+S△ANC=S△AOC=![]()
∵![]() ,且AO=AB,
,且AO=AB,
∴∠CAN+∠OAM=90°,∠AOM+∠OAM=90°,
∴∠AOM=∠CAN,
又∵∠AMO=∠CNA=90°,
∴△OAM∽△ACN,
∴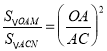
∵BC∶AC =1:3,
∴OA∶AC =4:3,
∴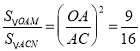
∴S△OAM=![]() =6
=6
∵点B在反比例函数![]()
![]() 的图象上,
的图象上,
∴S△OBM=![]() |k|,解得k=±12
|k|,解得k=±12
∵图象在第二象限,
.∴k=-12.
故答案为B.

【题目】在一次数学实践活动中,观测小组对某品牌节能饮水机进行了观察和记录,当观察到第![]() 分钟时,水温为
分钟时,水温为![]() ,记录的相关数据如下表所示:
,记录的相关数据如下表所示:
第一次加热、降温过程 | … | |||||||||||
t(分钟) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | … |
y( | 20 | 40 | 60 | 80 | 100 | 80 | 66.7 | 57.1 | 50 | 44.4 | 40 | … |
(饮水机功能说明:水温加热到![]() 时饮水机停止加热,水温开始下降,当降到
时饮水机停止加热,水温开始下降,当降到![]() 时饮水机又自动开始加热)
时饮水机又自动开始加热)
请根据上述信息解决下列问题:
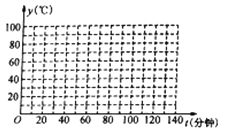
(1)根据表中数据在如给出的坐标系中,描出相应的点;
(2)选择适当的函数,分别求出第一次加热过程和第一次降温过程![]() 关于
关于![]() 的函数关系式,并写出相应自变量的取值范围;
的函数关系式,并写出相应自变量的取值范围;
(3)已知沏茶的最佳水温是![]() ,若18:00开启饮水机(初始水温
,若18:00开启饮水机(初始水温![]() )到当晚20:10,沏茶的最佳水温时间共有多少分钟?
)到当晚20:10,沏茶的最佳水温时间共有多少分钟?