题目内容
 如图,等腰△ABC中,AC=BC,CD是底边上的高,∠A=30°.
如图,等腰△ABC中,AC=BC,CD是底边上的高,∠A=30°.
(1)CD与AB有什么数量关系?请说明理由;
(2)过点D作DD1⊥BC,垂足为D1;D1D2⊥AB,垂足为D2;D2D3⊥BC,垂足为D3;D3D4⊥AB,垂足为D4;…;D2n+1D2n⊥AB,垂足为D2n;D2n+1D2n⊥BC,垂足为D2n+1(n为非零自然数).若CD=a,请用含a的代数式表示下表中线段的长度(请将结果直接填入表中);
| 线段 | D1D2 | D3D4 | D5D6 | … | D2n-1 D2n |
| 长度 |  | … |
解:(1)∵AC=BC,CD⊥AB,∴AD=BD= AB.
AB.
在Rt△ACD中, =tan30°,∴CD=ADtan30°=
=tan30°,∴CD=ADtan30°= AB×
AB× AB.
AB.
(2)填表依次为: (或
(或 或
或 ),
),
(或 或
或 ),
), (或
(或 )
)
(3)∵整个屋架有18根辅柱,
∴右侧最短一根辅柱为D8D9,倒数第二根为D7D8,
D8D9=D7D8cos30°=( )4a×cos30°=(
)4a×cos30°=( )4×
)4× AB×cos30°
AB×cos30°
=( )4×
)4× ×16×cos30°=
×16×cos30°= ≈1.3(米).
≈1.3(米).
答:最短一根辅柱的长度约为1.3米.
分析:(1)根据30°的正切值易得CD与AD之间的关系,而根据等腰三角形三线合一的性质可得AD等于BA的一半;
(2)易得∠DCB=60°,那么可根据60°的正弦值得到DD1= a;同理可得D1D2=(
a;同理可得D1D2=( )2a=
)2a= a,按规律可得D3D4=(
a,按规律可得D3D4=( )4a=
)4a= a,D5D6=(
a,D5D6=( )6a=
)6a= a,D2n-1D2n=(
a,D2n-1D2n=( )2na=(
)2na=( )na;
)na;
(3)易得DB=8,利用(2)得到的结论,可算出D7D8的长度,利用30°的余弦值可求得所求线段的长度.
点评:本题主要运用了等腰三角形的性质及锐角三角函数,注意总结规律的得出.
 AB.
AB.在Rt△ACD中,
 =tan30°,∴CD=ADtan30°=
=tan30°,∴CD=ADtan30°= AB×
AB× AB.
AB.(2)填表依次为:
 (或
(或 或
或 ),
),
(或
 或
或 ),
), (或
(或 )
)(3)∵整个屋架有18根辅柱,
∴右侧最短一根辅柱为D8D9,倒数第二根为D7D8,
D8D9=D7D8cos30°=(
 )4a×cos30°=(
)4a×cos30°=( )4×
)4× AB×cos30°
AB×cos30°=(
 )4×
)4× ×16×cos30°=
×16×cos30°= ≈1.3(米).
≈1.3(米).答:最短一根辅柱的长度约为1.3米.
分析:(1)根据30°的正切值易得CD与AD之间的关系,而根据等腰三角形三线合一的性质可得AD等于BA的一半;
(2)易得∠DCB=60°,那么可根据60°的正弦值得到DD1=
 a;同理可得D1D2=(
a;同理可得D1D2=( )2a=
)2a= a,按规律可得D3D4=(
a,按规律可得D3D4=( )4a=
)4a= a,D5D6=(
a,D5D6=( )6a=
)6a= a,D2n-1D2n=(
a,D2n-1D2n=( )2na=(
)2na=( )na;
)na;(3)易得DB=8,利用(2)得到的结论,可算出D7D8的长度,利用30°的余弦值可求得所求线段的长度.
点评:本题主要运用了等腰三角形的性质及锐角三角函数,注意总结规律的得出.

练习册系列答案
相关题目
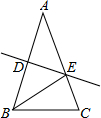 如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )
如图,等腰△ABC中,AB=AC,∠A=20°.线段AB的垂直平分线交AB于D,交AC于E,连接BE,则∠CBE等于( )| A、80° | B、70° | C、60° | D、50° |
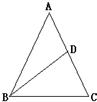 13、如图,等腰△ABC中,AB=AC,BD为腰AC的中线,将△ABC分成长12cm和9cm的两段,则等腰△ABC的腰长为
13、如图,等腰△ABC中,AB=AC,BD为腰AC的中线,将△ABC分成长12cm和9cm的两段,则等腰△ABC的腰长为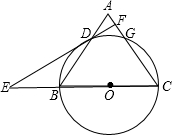 如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE=
如图,等腰△ABC中,AC=BC=10,AB=12,以BC为直径作⊙0交AB于D,交AC于G,DF⊥AC,垂足为F,交CB的延长线于点E,则sinE= 如图,等腰△ABC中,AB=AC,D为BC中点,E为射线AD上一点.
如图,等腰△ABC中,AB=AC,D为BC中点,E为射线AD上一点. 如图,等腰△ABC中,AB=AC,D、E分别为AC、AB的中点.
如图,等腰△ABC中,AB=AC,D、E分别为AC、AB的中点.