��Ŀ����
����Ŀ����֪����![]() ��ͬһ��ֱ���ϣ���
��ͬһ��ֱ���ϣ���![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣮
���е㣮
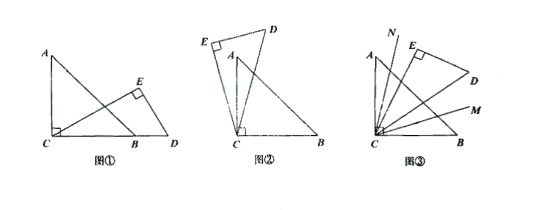
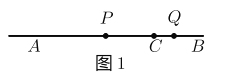
��1����ͼ1 ������![]() ���߶�
���߶�![]() ��ʱ��
��ʱ��
����![]() �����߶�
�����߶�![]() �ij�Ϊ_______��
�ij�Ϊ_______��
������![]() Ϊ�߶�
Ϊ�߶�![]() ������һ�㣬
������һ�㣬 ![]() �����߶�
�����߶�![]() �ij�Ϊ_______�� �� �ú�
�ij�Ϊ_______�� �� �ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2����ͼ2 ������![]() �����߶�
�����߶�![]() ��ʱ����
��ʱ����![]() ����
����![]() �ij����ú�
�ij����ú�![]() �Ĵ���ʽ��ʾ�� ��
�Ĵ���ʽ��ʾ�� ��
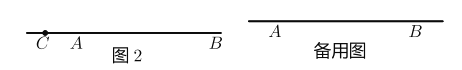
��3����ͼ����֪![]() ��������
��������![]() ��������
��������![]() ƽ��
ƽ��![]() ������
������![]() ƽ��
ƽ��![]() ��
��
�ٵ�����![]() ��
��![]() ���ڲ�ʱ����
���ڲ�ʱ����![]() =________�㣮
=________�㣮
�ڵ�����![]() ��
�� ![]() ���ⲿʱ����
���ⲿʱ����![]() =_______���� �� �ú�
=_______���� �� �ú�![]() �Ĵ���ʽ��ʾ�� ��
�Ĵ���ʽ��ʾ�� ��
���𰸡���1����5����![]() ����2��
����2�� ![]() ����3����
����3����![]() ����
����![]() ��
��
��������
(1) �������PC=4,QC=1�������߶�![]() �ij����ɣ�
�ij����ɣ�
�������PC= ![]() AC,QC=
AC,QC=![]() BC��������m��ʾ�߶�
BC��������m��ʾ�߶�![]() �ij���
�ij���
(2) ����![]() �����߶�
�����߶�![]() ��ʱ�������PC=
��ʱ�������PC= ![]() AC,QC=
AC,QC=![]() BC������ͼ����m��ʾ�߶�
BC������ͼ����m��ʾ�߶�![]() �ij����ɣ�
�ij����ɣ�
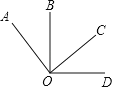
(3))���Ȱ������⻭��ͼ�Σ���OC�ڡ�AOB�ڲ����ⲿ����������������POC= ![]() ��AOC,��COQ=
��AOC,��COQ=![]() ��COB���ٸ���ͼ���ñ�ʾ
��COB���ٸ���ͼ���ñ�ʾ![]() ���ɣ�
���ɣ�
�⣺(1) �١�![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬
��PC=4,QC=1��
��PQ=PC+QC=5��
�ʴ�Ϊ5��
�ڵ�![]() Ϊ�߶�
Ϊ�߶�![]() ������һ�㣬
������һ�㣬 ![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬
��PC= ![]() AC,QC=
AC,QC=![]() BC��
BC��
��PQ=PC+QC=![]() AC+
AC+![]() BC=
BC=![]() AB=
AB=![]() m��
m��
�ʴ�Ϊ![]() m.
m.
(2)����C���߶�BA���ӳ���ʱ����ͼ2��
![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬
��PC= ![]() AC,QC=
AC,QC= ![]() BC��
BC��
��PQ=QC-PC=![]() BC-
BC-![]() AC=
AC=![]() AB=
AB=![]() m��
m��
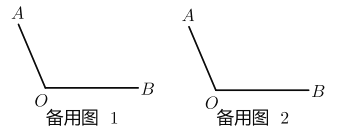
����C���߶�AB���ӳ���ʱ����ͼ3��
![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬
���е㣬
��PC= ![]() AC,QC=
AC,QC= ![]() BC��
BC��
��PQ=PC-QC=![]() AC-
AC-![]() BC=
BC=![]() AB=
AB=![]() m��
m��
�൱��![]() �����߶�
�����߶�![]() ��ʱ����
��ʱ����![]() ��
�� ![]() �ij�Ϊ
�ij�Ϊ![]() m.
m.
(3) �ٵ�����![]() ��
��![]() ���ڲ�ʱ����ͼ1��
���ڲ�ʱ����ͼ1��
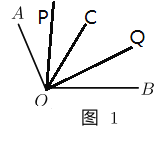
������![]() ƽ��
ƽ��![]() ������
������![]() ƽ��
ƽ��![]()
���POC= ![]() ��AOC,��COQ=
��AOC,��COQ=![]() ��COB��
��COB��
���POQ=��POC+��COQ= ![]() ��AOC+
��AOC+![]() ��COB =
��COB =![]() ��AOB=
��AOB=![]() ,
,
�ʴ�Ϊ![]() ;
;
�ڵ�����![]() ��
�� ![]() ���ⲿʱ����ͼ2
���ⲿʱ����ͼ2
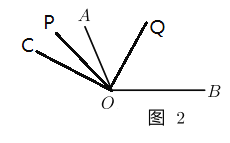
������![]() ƽ��
ƽ��![]() ������
������![]() ƽ��
ƽ��![]()
���POC= ![]() ��AOC,��COQ=
��AOC,��COQ=![]() ��COB��
��COB��
���POQ=��QOC-��COP= ![]() ��COB-
��COB-![]() ��AOC =
��AOC =![]() ��AOB=
��AOB=![]() ;
;
�ʴ�Ϊ![]() .
.