题目内容
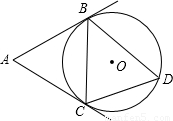
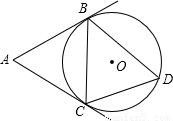
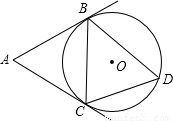
已知,如图,优弧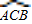 的度数为280°,D是由弦AB与优弧
的度数为280°,D是由弦AB与优弧 所围成的弓形区域内的任意点,连接AD、BD.试判断∠ADB的度数范围?并说明理由.
所围成的弓形区域内的任意点,连接AD、BD.试判断∠ADB的度数范围?并说明理由.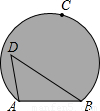
【答案】分析:延长AD与圆交于E,连接BE,由 的度数,求出
的度数,求出 所对圆心角的度数,根据圆周角定理:同弧所对的圆心角等于它所对圆周角的2倍,求出∠AEB的度数,再由∠ADB为三角形BDE的外角,利用三角形的外角性质可得∠ADB大于∠AEB,同时∠ADB小于平角,可得出∠ADB的度数范围.
所对圆心角的度数,根据圆周角定理:同弧所对的圆心角等于它所对圆周角的2倍,求出∠AEB的度数,再由∠ADB为三角形BDE的外角,利用三角形的外角性质可得∠ADB大于∠AEB,同时∠ADB小于平角,可得出∠ADB的度数范围.
解答:解:∠ADB的度数范围为:40°<∠ADB<180°,(2分)
理由为:延长AD交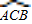 于E点,连接EB,(2分)
于E点,连接EB,(2分)
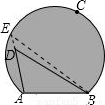
∵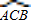 =280°,
=280°,
∴∠AEB= (360°-
(360°-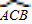 )=40°,(2分)
)=40°,(2分)
又∵∠ADB为△BDE的外角,
∴∠ADB=∠AEB+∠EBD>∠AEB,且∠ADB<180°,(2分)
则40°<∠ADB<180°.
(说理过程中结论完整不扣分,如最后结论不全则需倒扣1分)
点评:此题考查了圆心角、弧、弦的关系,圆周角定理,以及三角形的外角性质,解题的关键是延长AD,构造圆周角∠AEB,利用三角形的外角性质来解决问题.
 的度数,求出
的度数,求出 所对圆心角的度数,根据圆周角定理:同弧所对的圆心角等于它所对圆周角的2倍,求出∠AEB的度数,再由∠ADB为三角形BDE的外角,利用三角形的外角性质可得∠ADB大于∠AEB,同时∠ADB小于平角,可得出∠ADB的度数范围.
所对圆心角的度数,根据圆周角定理:同弧所对的圆心角等于它所对圆周角的2倍,求出∠AEB的度数,再由∠ADB为三角形BDE的外角,利用三角形的外角性质可得∠ADB大于∠AEB,同时∠ADB小于平角,可得出∠ADB的度数范围.解答:解:∠ADB的度数范围为:40°<∠ADB<180°,(2分)
理由为:延长AD交
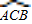 于E点,连接EB,(2分)
于E点,连接EB,(2分)
∵
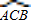 =280°,
=280°,∴∠AEB=
 (360°-
(360°-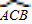 )=40°,(2分)
)=40°,(2分)又∵∠ADB为△BDE的外角,
∴∠ADB=∠AEB+∠EBD>∠AEB,且∠ADB<180°,(2分)
则40°<∠ADB<180°.
(说理过程中结论完整不扣分,如最后结论不全则需倒扣1分)
点评:此题考查了圆心角、弧、弦的关系,圆周角定理,以及三角形的外角性质,解题的关键是延长AD,构造圆周角∠AEB,利用三角形的外角性质来解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
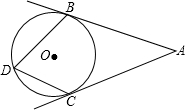 如图,AB、AC是⊙O的两条切线,切点分别为B、C,D是优弧
如图,AB、AC是⊙O的两条切线,切点分别为B、C,D是优弧