题目内容
(2012•红桥区二模)已知一抛物线经过O(0,0),B(1,1)两点,且解析式的二次项系数为-
(a>0).
(Ⅰ)当a=1时,求该抛物线的解析式,并用配方法求出该抛物线的顶点坐标;
(Ⅱ)已知点A(0,1),若抛物线与射线AB相交于点M,与x轴相交于点N(异于原点),当a在什么范围内取值时,ON+BM的值为常数?当a在什么范围内取值时,ON-BM的值为常数?
(Ⅲ)若点P(t,t)在抛物线上,则称点P为抛物线的不动点.将这条抛物线进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线y=x-
上,请说明理由.
| 1 |
| a |
(Ⅰ)当a=1时,求该抛物线的解析式,并用配方法求出该抛物线的顶点坐标;
(Ⅱ)已知点A(0,1),若抛物线与射线AB相交于点M,与x轴相交于点N(异于原点),当a在什么范围内取值时,ON+BM的值为常数?当a在什么范围内取值时,ON-BM的值为常数?
(Ⅲ)若点P(t,t)在抛物线上,则称点P为抛物线的不动点.将这条抛物线进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线y=x-
| a |
| 4 |
分析:(Ⅰ)首先利用抛物线经过O(0,0),B(1,1)两点,且解析式的二次项系数为-
求出抛物线解析式,再利用a=1求出抛物线的顶点坐标即可;
(Ⅱ)利用当y=0时,有-
x2+(1+
)x=0,求出x的值,进而得出点N的坐标,再利用若点M在点B右侧,此时a>1,BM=a-1;若点M在点B左侧,此时0<a<1,BM=1-a得出答案即可;
(Ⅲ)利用平移后的抛物线只有一个不动点,故此方程有两个相等的实数根,得出判别式△=(a-2h)2-4(h2-ak)=0,进而求出k与h,a的关系即可得出顶点(h,k)在直线y=x-
上.
| 1 |
| a |
(Ⅱ)利用当y=0时,有-
| 1 |
| a |
| 1 |
| a |
(Ⅲ)利用平移后的抛物线只有一个不动点,故此方程有两个相等的实数根,得出判别式△=(a-2h)2-4(h2-ak)=0,进而求出k与h,a的关系即可得出顶点(h,k)在直线y=x-
| a |
| 4 |
解答:解:设该抛物线的解析式为y=-
x2+bx+c,
∵抛物线经过(0,0)、(1,1)两点,
∴
,
解得
.
∴该抛物线的解析式为y=-
x2+(1+
)x
(Ⅰ)当a=1时,该抛物线的解析式为y=-x2+2x,
y=-x2+2x=-(x2-2x+1)+1=-(x-1)2+1.
该抛物线的顶点坐标为(1,1);
(Ⅱ)∵点N在x轴上,∴点N的纵坐标为0.
当y=0时,有-
x2+(1+
)x=0,
解得x1=0,x2=a+1.
∵点N异于原点,∴点N的坐标为(a+1,0).
∴ON=a+1,
∵点M在射线AB上,∴点M的纵坐标为1.
当y=1时,有-
x2+(1+
)x=1,
整理得出
x2-(1+
)x+1=0,
解得x1=1,x2=a.
点M的坐标为(1,1)或(a,1).
当点M的坐标为(1,1)时,M与B重合,
此时a=1,BM=0,ON=2.ON+BM与ON-BM的值都是常数2.
当点M的坐标为(a,1)时,
若点M在点B右侧,此时a>1,BM=a-1.
∴ON+BM=(a+1)+(a-1)=2a,ON-BM=(a+1)-(a-1)=2.
若点M在点B左侧,此时0<a<1,BM=1-a.
∴ON+BM=(a+1)+(1-a)=2,ON-BM=(a+1)-(1-a)=2a.
∴当0<a≤1时,ON+BM的值是常数2,
当a≥1时,ON-BM的值是常数2.
(Ⅲ)设平移后的抛物线的解析式为y=-
(x-h)2+k,
由不动点的定义,得方程:t=-
(t-h)2+k,
即t2+(a-2h)t+h2-ak=0.
∵平移后的抛物线只有一个不动点,∴此方程有两个相等的实数根.
∴判别式△=(a-2h)2-4(h2-ak)=0,
有a-4h+4k=0,即k=h-
.
∴顶点(h,k)在直线y=x-
上.
| 1 |
| a |
∵抛物线经过(0,0)、(1,1)两点,
∴
|
解得
|
∴该抛物线的解析式为y=-
| 1 |
| a |
| 1 |
| a |
(Ⅰ)当a=1时,该抛物线的解析式为y=-x2+2x,
y=-x2+2x=-(x2-2x+1)+1=-(x-1)2+1.
该抛物线的顶点坐标为(1,1);
(Ⅱ)∵点N在x轴上,∴点N的纵坐标为0.
当y=0时,有-
| 1 |
| a |
| 1 |
| a |
解得x1=0,x2=a+1.
∵点N异于原点,∴点N的坐标为(a+1,0).
∴ON=a+1,
∵点M在射线AB上,∴点M的纵坐标为1.
当y=1时,有-
| 1 |
| a |
| 1 |
| a |
整理得出
| 1 |
| a |
| 1 |
| a |
解得x1=1,x2=a.
点M的坐标为(1,1)或(a,1).
当点M的坐标为(1,1)时,M与B重合,
此时a=1,BM=0,ON=2.ON+BM与ON-BM的值都是常数2.
当点M的坐标为(a,1)时,
若点M在点B右侧,此时a>1,BM=a-1.
∴ON+BM=(a+1)+(a-1)=2a,ON-BM=(a+1)-(a-1)=2.
若点M在点B左侧,此时0<a<1,BM=1-a.
∴ON+BM=(a+1)+(1-a)=2,ON-BM=(a+1)-(1-a)=2a.
∴当0<a≤1时,ON+BM的值是常数2,
当a≥1时,ON-BM的值是常数2.
(Ⅲ)设平移后的抛物线的解析式为y=-
| 1 |
| a |
由不动点的定义,得方程:t=-
| 1 |
| a |
即t2+(a-2h)t+h2-ak=0.
∵平移后的抛物线只有一个不动点,∴此方程有两个相等的实数根.
∴判别式△=(a-2h)2-4(h2-ak)=0,
有a-4h+4k=0,即k=h-
| a |
| 4 |
∴顶点(h,k)在直线y=x-
| a |
| 4 |
点评:此题主要考查了二次函数的综合应用以及根的判别式的性质等知识,利用分类讨论的思想得出M与B的不同位置关系得出答案是解题关键.

练习册系列答案
相关题目
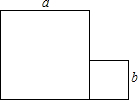 (2012•红桥区二模)已知两个正方形的边长分别为a、b,如图,将这两个正方形拼在一起.问能否将此图适当分割,重新拼成一个正方形,使其面积等于已知两个正方形面积的和:
(2012•红桥区二模)已知两个正方形的边长分别为a、b,如图,将这两个正方形拼在一起.问能否将此图适当分割,重新拼成一个正方形,使其面积等于已知两个正方形面积的和: (2012•红桥区二模)如图所示,⊙O中,OA⊥BC,垂足为H,∠AOB=50°,则圆周角∠ADC的度数是( )
(2012•红桥区二模)如图所示,⊙O中,OA⊥BC,垂足为H,∠AOB=50°,则圆周角∠ADC的度数是( ) 送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4米.
送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4米.