题目内容
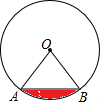如图，在⊙O中，弧AB=60°，AB=6，
（1）求圆的半径；
（2）求弧AB的长；
（3）求阴影部分的面积．
解：（1）∵弧AB=60°，
∴∠AOB=60°
又∵OA=OB，
∴△OAB是等边三角形，
∴OA=AB=6；
（2）弧AB的长l=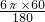
=2π；
（3）等边△AOB的面积是：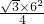
=9
，
S扇形OAB=
=6π，
则S阴影=S扇形OAB-S△OAB=6π-9．
分析：（1）易证△OAB是等边三角形，即可求得；
（2）利用弧长公式即可直接求解；
（3）根据扇形的面积公式求得扇形OAB的面积减去△OAB的面积即可求得．
点评：本题考查了弧长公式和扇形的面积公式，正确理解公式是关键．
∴∠AOB=60°
又∵OA=OB，
∴△OAB是等边三角形，
∴OA=AB=6；
（2）弧AB的长l=
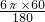=2π；（3）等边△AOB的面积是：
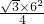=9，S扇形OAB=
=6π，则S阴影=S扇形OAB-S△OAB=6π-9
．分析：（1）易证△OAB是等边三角形，即可求得；
（2）利用弧长公式即可直接求解；
（3）根据扇形的面积公式求得扇形OAB的面积减去△OAB的面积即可求得．
点评：本题考查了弧长公式和扇形的面积公式，正确理解公式是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
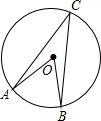如图，在⊙O中，弧AB=50°，则圆周角∠ACB的大小为（ ）| A、25° | B、50° | C、100° | D、130° |
作PM∥AB交DC的延长线于M，
如图，在⊙M中，弧AB所对的圆心角为120°，已知⊙M的半径为2cm，并建立如图所示的直角坐标系．
如图，在⊙O中，弧AB=60°，AB=6，