Question

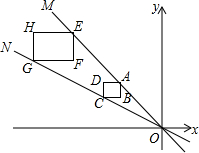（2013•苏州一模）正方形ABCD，矩形EFGH均位于第二象限内，它们的边平行于x轴或y轴，其中点A，E在直线OM上，点C，G在直线ON上，O为坐标原点，点A的坐标为（-3，3），正方形ABCD的边长为1．若矩形EFGH（GF＞EF）的周长为14，面积为12，则点F的坐标为

（-10，7）

．

Answer 1

分析：先根据A的坐标为（-3，3），正方形ABCD的边长为1得出直线OM的解析式，再求出C点的坐标利用待定系数法即可求出直线ON的解析式；设矩形EFGH的宽为a，则长为7-a，再根据面积为12即可得出a的值，由点E在直线OM上设点E的坐标为（e，e），由矩形的边长可用e表示出F、G点的坐标，再根据G点在直线ON上即可得出e的值，进而得出结论．

解答：解：∵A的坐标为（-3，3），
∴直线OM的解析式为y=-x，
∵正方形ABCD的边长为1，
∴C（-4，2），
设直线ON的解析式为y=kx（k≠0），
∴2=-4k，解得k=-

1

2

，
∴直线ON的解析式为：y=-

1

2

x；
设矩形EFGH的宽为a，则长为7-a，
∵矩形EFGH的面积为12，
∴a（7-a）=12，
解得a=3或a=4，
当a=3即EF=3时，EH=7-3=4，
∵点E在直线OM上，设点E的坐标为（-e，e），
∴F（-e，e-3），G（-e-4，e-3），
∵点G在直线ON上，
∴e-3=-

1

2

（-e-4），解得e=10，
∴F（-10，7）；
当a=4即EF=4时，EH=7-4=3（不合题意舍去）．
故答案为：（-10，7）．

点评：本题考查的是一次函数综合题，根据题意得出直线ON的解析式是解答此题的关键，在解答时要注意进行分类讨论．