题目内容
【题目】小聪和小明沿同一条路同时从学校出发到学校图书馆查阅资料,学校与图书馆的路程是![]() 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到达图书馆,图中折线![]() 和线段
和线段![]() 分别表示两人离学校的路程
分别表示两人离学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系,请根据图象回答下列问题:
(分钟)之间的函数关系,请根据图象回答下列问题:
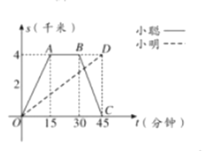
(1)小聪在图书馆查阅资料的时间为 分钟,小聪返回学校的速度为 千米/分钟;
(2)请你求出小明离开学校的路程![]() (千米)与所经过的时间
(千米)与所经过的时间![]() (分钟)之间的函数关系;
(分钟)之间的函数关系;
(3)求线段![]() 的函数关系式;
的函数关系式;
(4)当小聪与小明迎面相遇时,他们离学校的路程是多少千米?
【答案】(1)15;![]() ;(2)s与t的函数关系式s=
;(2)s与t的函数关系式s=![]() t(0≤t≤45).(3)线段
t(0≤t≤45).(3)线段![]() 的函数解析式为s=-
的函数解析式为s=- ![]() t+12(30≤t≤45);(4)3千米
t+12(30≤t≤45);(4)3千米
【解析】
(1)直接根据图象上所给的数据的实际意义可求解;
(2)由图象可知,s是t的正比例函数,设所求函数的解析式为s=kt(k≠0),把(45,4)代入解析式利用待定系数法即可求解;
(3)由图象可知,小聪在30≤t≤45的时段内s是t的一次函数,设线段![]() 的函数解析式为s=mt+n(m≠0)把(30,4),(45,0)代入利用待定系数法先求得函数关系式,
的函数解析式为s=mt+n(m≠0)把(30,4),(45,0)代入利用待定系数法先求得函数关系式,
(4)根据求函数图象的交点方法求得函数交点坐标即可.
(1)∵3015=15,4÷15=![]()
∴小聪在天一阁查阅资料的时间和小聪返回学校的速度分别是15分钟,![]() 千米/分钟.
千米/分钟.
故答案为:15;![]() ;
;
(2)由图象可知,s是t的正比例函数
设所求函数的解析式为s=kt(k≠0)
代入(45,4),得
4=45k
解得k=![]()
∴s与t的函数关系式s=![]() t(0≤t≤45).
t(0≤t≤45).
(3)由图象可知,小聪在30≤t≤45的时段内s是t的一次函数,设线段![]() 的函数解析式为s=mt+n(m≠0)
的函数解析式为s=mt+n(m≠0)
代入(30,4),(45,0),得![]()
解得
∴s=- ![]() t+12(30≤t≤45),
t+12(30≤t≤45),
即线段![]() 的函数解析式为s=-
的函数解析式为s=- ![]() t+12(30≤t≤45);
t+12(30≤t≤45);
(4)令-![]() t+12=
t+12=![]() t,解得t=
t,解得t=![]()
当t=![]() 时,S=
时,S=![]() ×
×![]() =3.
=3.
答:当小聪与小明迎面相遇时,他们离学校的路程是3千米.

【题目】甲、乙两名队员参加设计训练,成绩分别被制成下列两个统计图:
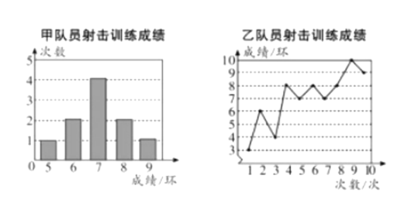
根据以上信息,整理分析数据如下:
平均数(环) | 中位数(环) | 众数(环) | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)表格中![]() ,
,![]() ,
,![]() ;
;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?
(3)如果乙再射击![]() 次,命中
次,命中![]() 环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)
环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)