Question

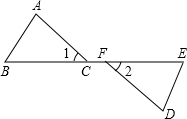（2012•河东区二模）如图，点B，C，F，E在同一直线上，∠1=∠2，BC=FE，要使△ABC≌△DEF，还需添加一个条件，这个条件可以

AC=DF或∠A=∠D或∠B=∠E

（只需写出一个）．

Answer 1

分析：若添的条件是AC=DF，利用SAS可得出△ABC≌△DEF；若添的条件是∠A=∠D，利用AAS可得出△ABC≌△DEF；若添的条件是∠B=∠E，利用ASA可得出△ABC≌△DEF．

解答：解：若添的条件为AC=DF，
在△ABC和△DEF中，
∵

AC=DF ∠1=∠2 BC=EF

，
∴△ABC≌△DEF（SAS）；
若添的条件是∠A=∠D，
在△ABC和△DEF中，
∵

∠A=∠D ∠1=∠2 BC=EF

，
∴△ABC≌△DEF（AAS）；
若添的条件是∠B=∠E，
在△ABC和△DEF中，
∵

∠B=∠E BC=EF ∠1=∠2

，
∴△ABC≌△DEF（ASA）．
故答案为：AC=DF或∠A=∠D或∠B=∠E．

点评：此题考查了全等三角形的判定，全等三角形的判定方法有：SSS；SAS；ASA；AAS，以及HL（直角三角形判定全等的方法），熟练掌握全等三角形的判定方法是解本题的关键．