题目内容

抛物线y=x2+bx+c过点（-3，0），（1，0），则该抛物线的对称轴为
 
．
分析：根据抛物线的对称性，抛物线上纵坐标相同的两点的连线被对称轴垂直平分，对称轴是：x=
x1+x2
2
．
解答：解：∵点（-3，0），（1，0），的纵坐标相同，
∴这两点一定关于对称轴对称，
∴对称轴是：x=
-3+1
2
，即x=-1．
点评：能够认识到已知的两点关于对称轴对称是解决本题的关键．
练习册系列答案
相关题目
已知Pi（i=1，2，3，4）是抛物线y=x2+bx+1上共圆的四点，它们的横坐标分别为xi（i=1，2，3，4），又xi（i=1，2，3，4）是方程（x2-4x+m）（x2-4x+n）=0的根，则二次函数y=x2+bx+1的最小值为（　　）
A、-1B、-2C、-3D、-4
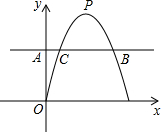直线AB平行于x轴，与y轴交于点A（0，a），AB=a，经过原点的抛物线y=-x2+bx经过点B，精英家教网且与直线AB交于另一点C（在B的左边），抛物线的顶点为P．
（1）求抛物线的解析式（用含a的代数式表示）；
（2）用含a的式子表示BC的长；
（3）当a为何值时，△PCB是等腰直角三角形？当a为何值时△PCB是等边三角形？
已知抛物线y=x2+bx+c，经过点A（0，5）和点B（3，2）
（1）求抛物线的解析式：
（2）现有一半径为l，圆心P在抛物线上运动的动圆，问⊙P在运动过程中，是否存在⊙P与坐标轴相切的情况？若存在，请求出圆心P的坐标：若不存在，请说明理由．
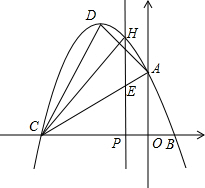精英家教网已知：m，n是方程x2-6x+5=0的两个实数根，且m＜n，抛物线y=-x2+bx+c的图象经过点B（m，0），A（0，n）
（1）求这条抛物线的解析式；
（2）（1）中的抛物线与x轴的另一个交点为C，顶点为D，求出C，D的坐标和△ACD的面积；
（3）P是线段OC上的一点，过点P作PH⊥x轴，与抛物线交于H点，交AC于F点，如直线AC把△PCH分成面积1：3的两部分，请求出P点的坐标．
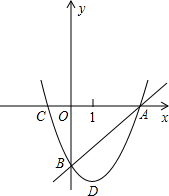（2013•普陀区二模）如图，抛物线y=x2+bx-c经过直线y=x-3与坐标轴的两个交点A、B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．
（1）求此抛物线的解析式；
（2）点P为抛物线上的一个动点，求使S△APC：S△ACD=5：4的点P的坐标；
（3）点M为平面直角坐标系上一点，写出使点M、A、B、D为平行四边形的点M的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网