Question

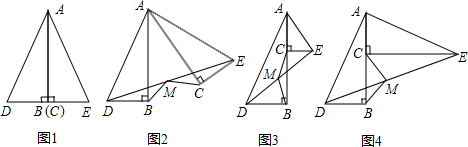
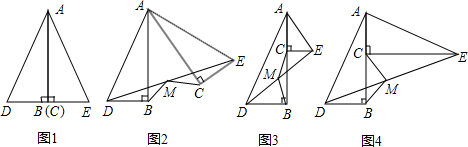
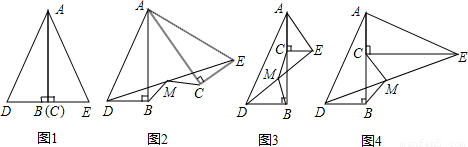
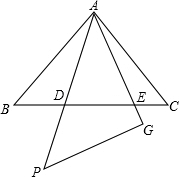如图，将两个全等的等腰直角三角形摆成如图所示的样子（顶点A重合），
①请在图中找出三对相似但不全等的三角形．
②你认为AE²=ED•EB吗？请说明理由．

Answer 1

分析：（1）根据相似（不包括全等）三角形的判定可以得出△ADE∽△BAE，△CDA∽△ADE．
（2）由于△BAC和△AGF都是等腰直角三角形，因此∠B=∠PAG=45°，可得出∠BAE=∠ADE=45°+∠BAD；已知了△EAD和△EBA中，∠AED是公共角，可得出两三角形相似，即可得出结论．

解答：（1）解：△ADE∽△BAE，△CDA∽△ADE，△BAE∽△CDA．
∵△BAC和△AGP都是等腰直角三角形，
∴∠B=∠PAG=45°，
∴∠BAE=∠ADE=45°+∠BAD；
∵△EAD和△EBA中，∠AED是公共角，
∴△ADE∽△BAE；
同理，可得△CDA∽△ADE．
∴△BAE∽△CDA．

（2）证明：∵∠DAE=∠B=45°，∠AED=∠BEA，
∴△ADE∽△BAE，
∴

AE

BE

=

DE

AE

，
∴AE²=ED•EB．

点评：本题考查了相似三角形的判定与性质和等腰直角三角形，学生应熟练掌握两角法，判定三角形相似．