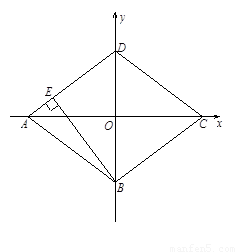��Ŀ����
 ��ֱ֪������ϵ������ABCD��λ����ͼ��C��D���������ֱ�Ϊ��4��0������0��3��������������P��Q�ֱ��A��Cͬʱ��������P���߶�AD���յ�D�˶�����Q������CBA���յ�A�˶������˶�ʱ��Ϊt�룮
��ֱ֪������ϵ������ABCD��λ����ͼ��C��D���������ֱ�Ϊ��4��0������0��3��������������P��Q�ֱ��A��Cͬʱ��������P���߶�AD���յ�D�˶�����Q������CBA���յ�A�˶������˶�ʱ��Ϊt�룮��1����գ�����ABCD�ı߳���
��2��̽���������⣺
������P���ٶ�Ϊÿ��1����λ����Q���ٶ�Ϊÿ��2����λ������Q���߶�BA��ʱ�����APQ�����S����t�ĺ�����ϵʽ���Լ�S�����ֵ��
������P���ٶ�Ϊÿ��1����λ����Q���ٶȱ�Ϊÿ��k����λ�����˶������У��κ�ʱ�̶�����Ӧ��kֵ��ʹ�á�APQ������һ�߷��ۣ�����ǰ��������������ɵ��ı���Ϊ���Σ���̽����t=4��ʱ�����Σ������k��ֵ��
��������1����֪C��D�����꣬����Rt��COD���ù��ɶ������CD�ij������εı߳������ε��������4��Rt��COD�������BE�ij��������ε���������εı߳�����ã�
��2�������APQ������ؼ�������ױ�AP�ϵĸߣ���Q��QG��AD��G����ôQG���ǡ�APQ�ĸߣ��ɸ������������Ρ�AQG�͡�ABE�����QG�ij���Ȼ����������ε�������㷽�����ɵó�����S��t�ĺ�����ϵʽ��Ȼ����ݵó��ĺ��������ʼ��ɵó�S�����ֵ���Լ���Ӧ��t��ֵ��
����Ҫʹ��APQ������һ�߷��ۣ�����ǰ���������������ɵ��ı���Ϊ���Σ���ô��APQ�����������Ϊ��APQΪ���������Σ���˿ɷ���������������ۣ�
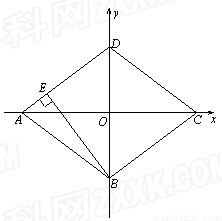
��һ���������Q��CB��ʱ��ͼ2����
����AP=4��BE����BE��AD��BC�����̵��߶Σ����ֻ��һ�������AQ=PQ���ɷ��ն��ķ���������Q1��Q1M��AP������Ϊ��M��Q1M��AC�ڵ�F����ͨ�����������Ρ�AMF�ס�AOD�ס�CQ1F�����FM�ij�����Q1M=BE����˿����Q1F�ij�����ֱ��������CQ1F�У��ɸ��ݡ�ACB������ֵ���CQ1�ij���Ȼ�����t=4�������k��ֵ��
�ڶ����������Q��AB��ʱ��
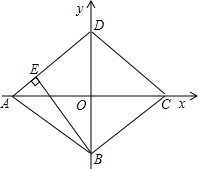
һ��AP=AQ��ͼ3������ʱP��Q2����x��Գƣ���֪��AP=t=4�����Q�˶���·��ΪCB+AB-AP=6������t=4�������k��ֵ��
����AP=PQ��ͼ4���������P��PM��AB��B����ô��ANP�ס�AEB���ɸ������Ƶó��ı����߶����AN�ij���Ҳ�������AQ3�ij���Ȼ�����һ�ķ������k��ֵ��
��2�������APQ������ؼ�������ױ�AP�ϵĸߣ���Q��QG��AD��G����ôQG���ǡ�APQ�ĸߣ��ɸ������������Ρ�AQG�͡�ABE�����QG�ij���Ȼ����������ε�������㷽�����ɵó�����S��t�ĺ�����ϵʽ��Ȼ����ݵó��ĺ��������ʼ��ɵó�S�����ֵ���Լ���Ӧ��t��ֵ��
����Ҫʹ��APQ������һ�߷��ۣ�����ǰ���������������ɵ��ı���Ϊ���Σ���ô��APQ�����������Ϊ��APQΪ���������Σ���˿ɷ���������������ۣ�
��һ���������Q��CB��ʱ��ͼ2����
����AP=4��BE����BE��AD��BC�����̵��߶Σ����ֻ��һ�������AQ=PQ���ɷ��ն��ķ���������Q1��Q1M��AP������Ϊ��M��Q1M��AC�ڵ�F����ͨ�����������Ρ�AMF�ס�AOD�ס�CQ1F�����FM�ij�����Q1M=BE����˿����Q1F�ij�����ֱ��������CQ1F�У��ɸ��ݡ�ACB������ֵ���CQ1�ij���Ȼ�����t=4�������k��ֵ��
�ڶ����������Q��AB��ʱ��
һ��AP=AQ��ͼ3������ʱP��Q2����x��Գƣ���֪��AP=t=4�����Q�˶���·��ΪCB+AB-AP=6������t=4�������k��ֵ��
����AP=PQ��ͼ4���������P��PM��AB��B����ô��ANP�ס�AEB���ɸ������Ƶó��ı����߶����AN�ij���Ҳ�������AQ3�ij���Ȼ�����һ�ķ������k��ֵ��
��� �⣺��1������ABCD�ı߳���5�������24����BE�ij���
�⣺��1������ABCD�ı߳���5�������24����BE�ij���
��
��2���������⣬��AP=t��AQ=10-2t��
��ͼ1������Q��QG��AD������ΪG����QG��BE�á�AQG�ס�ABE��
��
=
��
��QG=
-
��
��S=
AP•QG=-
t2+
t
��
��t��5����
��S=-
��t-
��2+6��
��t��5����
�൱t=
ʱ��S���ֵΪ6��
��Ҫʹ��APQ������һ�߷��ۣ�����ǰ���������������ɵ��ı���Ϊ���Σ�������ԳƵ����ʣ�ֻ���APQΪ���������μ��ɣ�
 ��t=4��ʱ���ߵ�P���ٶ�Ϊÿ��1����λ����AP=4��
��t=4��ʱ���ߵ�P���ٶ�Ϊÿ��1����λ����AP=4��
���·�����������ۣ�
��һ�����������Q��CB��ʱ��
��PQ��BE��PA����ֻ���ڵ�Q1��ʹQ1A=Q1P��
��ͼ2������Q1��Q1M��AP������Ϊ��M��Q1M��AC�ڵ�F����AM=
AP=2��
�ɡ�AMF�ס�AOD�ס�CQ1F����
=
=
=
��
��FM=
��
��Q1F=MQ1-FM=
��
��CQ1=
Q1F=
����
=
����k=
=
��
 �ڶ������������Q��BA��ʱ����������Q2��Q3��
�ڶ������������Q��BA��ʱ����������Q2��Q3��
�ֱ�ʹAP=AQ2��PA=PQ3��
i����AP=AQ2����ͼ3��CB+BQ2=10-4=6��
��
=
��
��k=
=
��
ii����PA=PQ3����ͼ4������P��PN��AB������ΪN��
�ɡ�ANP�ס�AEB����
=
��
��AE=
=
��
 ��AN=
��AN=
��
��AQ3=2AN=
��
��BC+BQ3=10-
=
��
=
��
��k=
=
��
������������t=4�룬�����õĵ���������APQ
�صױ߷��ۣ����ۺ�õ����ε�kֵΪ
��
��
��
 �⣺��1������ABCD�ı߳���5�������24����BE�ij���
�⣺��1������ABCD�ı߳���5�������24����BE�ij���| 24 |
| 5 |
��2���������⣬��AP=t��AQ=10-2t��
��ͼ1������Q��QG��AD������ΪG����QG��BE�á�AQG�ס�ABE��
��
| QG |
| BE |
| QA |
| BA |
��QG=
| 48 |
| 5 |
| 48t |
| 25 |
��S=
| 1 |
| 2 |
| 24 |
| 25 |
| 24 |
| 5 |
��
| 5 |
| 2 |
��S=-
| 24 |
| 25 |
| 5 |
| 2 |
| 5 |
| 2 |
�൱t=
| 5 |
| 2 |
��Ҫʹ��APQ������һ�߷��ۣ�����ǰ���������������ɵ��ı���Ϊ���Σ�������ԳƵ����ʣ�ֻ���APQΪ���������μ��ɣ�
 ��t=4��ʱ���ߵ�P���ٶ�Ϊÿ��1����λ����AP=4��
��t=4��ʱ���ߵ�P���ٶ�Ϊÿ��1����λ����AP=4�����·�����������ۣ�
��һ�����������Q��CB��ʱ��
��PQ��BE��PA����ֻ���ڵ�Q1��ʹQ1A=Q1P��
��ͼ2������Q1��Q1M��AP������Ϊ��M��Q1M��AC�ڵ�F����AM=
| 1 |
| 2 |
�ɡ�AMF�ס�AOD�ס�CQ1F����
| FM |
| AM |
| Q1F |
| CQ1 |
| OD |
| AO |
| 3 |
| 4 |
��FM=
| 3 |
| 2 |
��Q1F=MQ1-FM=
| 33 |
| 10 |
��CQ1=
| 4 |
| 3 |
| 22 |
| 5 |
| 1��t |
| k•t |
| AP |
| CQ1 |
| CQ1 |
| AP |
| 11 |
| 10 |
 �ڶ������������Q��BA��ʱ����������Q2��Q3��
�ڶ������������Q��BA��ʱ����������Q2��Q3���ֱ�ʹAP=AQ2��PA=PQ3��
i����AP=AQ2����ͼ3��CB+BQ2=10-4=6��
��
| 1��t |
| k•t |
| AP |
| CB+BQ2 |
��k=
| CB+BQ2 |
| AP |
| 3 |
| 2 |
ii����PA=PQ3����ͼ4������P��PN��AB������ΪN��
�ɡ�ANP�ס�AEB����
| AN |
| AE |
| AP |
| AB |
��AE=
| AB2-BE2 |
| 7 |
| 5 |
 ��AN=
��AN=| 28 |
| 25 |
��AQ3=2AN=
| 56 |
| 25 |
��BC+BQ3=10-
| 56 |
| 25 |
| 194 |
| 25 |
��
| 1��t |
| k•t |
| AP |
| CB+BQ3 |
��k=
| CB+BQ3 |
| AP |
| 97 |
| 50 |
������������t=4�룬�����õĵ���������APQ
�صױ߷��ۣ����ۺ�õ����ε�kֵΪ
| 11 |
| 10 |
| 3 |
| 2 |
| 97 |
| 50 |
������������Ҫ���������ε����ʣ�ͼ�εķ��۱任�����������ε������Լ����κ�����֪ʶ�㣬Ҫע�⣨3���У�Ҫ��Q��λ�õIJ�ͬ������������ۣ���Ҫ©�⣮

��ϰ��ϵ�д�
 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
�����Ŀ