ƒøƒ⁄»ð
°æƒø°ø»ÁÕº£¨Àƒ±þ–Œ![]() ÷–£¨µ„
÷–£¨µ„![]() Œ™÷±Ω«◊¯±Íœµµƒ‘≠µ„£¨
Œ™÷±Ω«◊¯±Íœµµƒ‘≠µ„£¨![]() µƒ◊¯±Í∑÷±Œ™
µƒ◊¯±Í∑÷±Œ™![]() £Æµ„
£Æµ„![]() Õ¨ ±¥”‘≠µ„≥ˆ∑¢£¨∑÷±◊˜‘»ÀŸ‘À∂Ø£¨µ„
Õ¨ ±¥”‘≠µ„≥ˆ∑¢£¨∑÷±◊˜‘»ÀŸ‘À∂Ø£¨µ„![]() —ÿ
—ÿ![]() “‘√ø√Î1∏ˆµ•ŒªœÚ÷’µ„
“‘√ø√Î1∏ˆµ•ŒªœÚ÷’µ„![]() ‘À∂Ø£¨µ„
‘À∂Ø£¨µ„![]() —ÿ
—ÿ![]() “‘√ø√Î2∏ˆµ•ŒªœÚ÷’µ„
“‘√ø√Î2∏ˆµ•ŒªœÚ÷’µ„![]() ‘À∂أƵ±’‚¡Ωµ„÷–”–“ªµ„µΩ¥Ô◊‘º∫µƒ÷’µ„ ±£¨¡Ì“ªµ„“≤Õ£÷π‘À∂أƅˑÀ∂Ø ±º‰Œ™
‘À∂أƵ±’‚¡Ωµ„÷–”–“ªµ„µΩ¥Ô◊‘º∫µƒ÷’µ„ ±£¨¡Ì“ªµ„“≤Õ£÷π‘À∂أƅˑÀ∂Ø ±º‰Œ™![]() √ΣÆ
√ΣÆ

£®1£©«Î”√![]() ±Ì 浄
±Ì 浄![]() µƒ◊¯±ÍŒ™__________£ª
µƒ◊¯±ÍŒ™__________£ª
£®2£© «∑ҥʑ⁄ƒ≥∏ˆ ±º‰![]() £¨ πµ√“‘µ„
£¨ πµ√“‘µ„![]() ∫ÕÀƒ±þ–Œ
∫ÕÀƒ±þ–Œ![]() ÷–µƒ»Œ“‚¡Ω∏ˆ∂•µ„Œ™∂•µ„µƒÀƒ±þ–ŒŒ™∆Ω––Àƒ±þ–Œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆ
÷–µƒ»Œ“‚¡Ω∏ˆ∂•µ„Œ™∂•µ„µƒÀƒ±þ–ŒŒ™∆Ω––Àƒ±þ–Œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆ![]() µƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©¥Ê‘⁄£¨
£ª£®2£©¥Ê‘⁄£¨![]() µƒ÷µŒ™6ªÚ
µƒ÷µŒ™6ªÚ![]() £Æ
£Æ
°æΩ‚Œˆ°ø
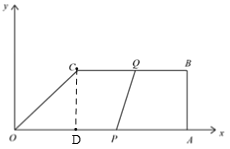
£®1£©∏˘æðA°¢B°¢C»˝µ„◊¯±Íø…«Û≥ˆOA°¢AB°¢BCµƒ≥§£¨π˝µ„C◊˜CD°ÕOA£¨‘ÚÀƒ±þ–ŒCDAB «æÿ–Œ£¨¿˚”√π¥π…∂®¿Ìø…«Û≥ˆOCµƒ≥§£¨¿˚”√æý¿Î=ÀŸ∂»°¡ ±º‰º¥ø…µ√¥∞∏£ª
£®2£©∑÷P°¢Q¡Ωµ„∑÷±”ÎO°¢C£ªA°¢B£ªP°¢Q£ªC°¢AÀƒ÷÷«Èøˆ£¨∏˘æð∆Ω––Àƒ±þ–Œµ√–‘÷ ∑÷±«Û≥ˆt÷µ£¨∏˘æðt°Ð9º∞µ„QÀ˘‘⁄Œª÷√≈–∂œº¥ø…µ√¥∞∏£Æ
£®1£©°þ![]() µƒ◊¯±Í∑÷±Œ™
µƒ◊¯±Í∑÷±Œ™![]() £¨
£¨
°ýOA=16£¨AB=6£¨BC=8£¨
π˝µ„C◊˜CD°ÕOA£¨‘ÚÀƒ±þ–ŒCDAB «æÿ–Œ£¨
°ýCD=AB=6£¨OD=OA-BC=8£¨
°ý![]() £¨◊Ð ±º‰
£¨◊Ð ±º‰![]() £®s£©£¨
£®s£©£¨
°þµ„QµƒÀŸ∂»Œ™√ø√Î2∏ˆµ•Œª£¨
°ýµ±![]() ±£¨
±£¨![]() £¨¥À ±µ„
£¨¥À ±µ„![]() ‘⁄
‘⁄![]() …œ£¨
…œ£¨![]() £¨
£¨
°ýµ„Qµƒ∫·◊¯±ÍŒ™OD+CQ=2t-10+8=2t-2£¨◊ð◊¯±ÍŒ™6£¨
°ýQµ„◊¯±ÍŒ™![]() £¨
£¨
π ¥∞∏Œ™£∫£®2t-2£¨6£©
£®2£©¢Ÿµ±P°¢Q”ÎO°¢Cππ≥…∆Ω––Àƒ±þ–Œ ±£¨‘ÚOP=CQ£¨
°þµ„PÀŸ∂»Œ™√ø√Î1∏ˆµ•Œª£¨
°ýOP=t£¨
°þCQ=2t-10£¨
°ý![]() £¨
£¨
Ω‚µ√£∫![]() ”Î
”Î![]() √¨∂У®…·£©£¨
√¨∂У®…·£©£¨
¢⁄P°¢Q”ÎA°¢Bππ≥…∆Ω––Àƒ±þ–Œ ±£¨‘ÚPA=QB£¨
°þOC=10£¨BC=8£¨
°ýQB=18-2t£¨
°þPA=16-t£¨
°ý![]() £¨
£¨
Ω‚µ√£∫![]() £¨¥À ±
£¨¥À ±![]() ‘⁄
‘⁄![]() …œ£¨≤ª∑˚∫œÃ‚“‚£¨…·»•
…œ£¨≤ª∑˚∫œÃ‚“‚£¨…·»•
¢€µ±P°¢Q”ÎO°¢Bππ≥…∆Ω––Àƒ±þ–Œ ±£¨‘ÚOP=QB£¨
°þOP=t£¨QB=18-2t£¨
![]() £¨
£¨
Ω‚µ√£∫![]() £¨∑˚∫œÃ‚“‚£¨
£¨∑˚∫œÃ‚“‚£¨
¢ÐP°¢Q”ÎC°¢Aππ≥…∆Ω––Àƒ±þ–Œ ±£¨‘ÚPA=CQ£¨
°þPA=16-t£¨CQ=2t-10£¨
°ý![]() £¨
£¨
Ω‚µ√![]() £¨∑˚∫œÃ‚“‚£¨
£¨∑˚∫œÃ‚“‚£¨
◊€…œÀ˘ ˆ£¨![]() µƒ÷µŒ™6ªÚ
µƒ÷µŒ™6ªÚ![]() £Æ
£Æ

 Ω≈∆ΩÃ∏®≈ý”≈”≈—°æÌ∆⁄ƒ©≥Â¥Ã100∑÷œµ¡–¥∞∏
Ω≈∆ΩÃ∏®≈ý”≈”≈—°æÌ∆⁄ƒ©≥Â¥Ã100∑÷œµ¡–¥∞∏







