��Ŀ����
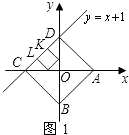
����Ŀ����֪��A��B�ֱ���x�ᡢy���ϵĶ��㣬��C��D��ij������ͼ���ϵĵ㣬���ı���ABCD��A��B��C��D�����������У�Ϊ������ʱ�������������Ϊ�˺���ͼ��İ��������Σ����磺��ͼ��������ABCD��һ�κ���y=x+1ͼ�������һ�����������Σ�
��1����ij������һ�κ���y=x+1��������ͼ������а��������εı߳���
��2����ij�����Ƿ���������y= ![]() ��k��0��������ͼ��İ���������ΪABCD����D��2��m����m��2���ڷ���������ͼ���ϣ���m��ֵ����������������ʽ��
��k��0��������ͼ��İ���������ΪABCD����D��2��m����m��2���ڷ���������ͼ���ϣ���m��ֵ����������������ʽ��
��3����ij�����Ƕ��κ���y=ax2+c��a��0��������ͼ��İ���������ΪABCD��C��D�е�һ��������Ϊ��3��4����д���������������������ϵ���һ���������� �� д���������������һ�������߽���ʽ �� ���ж���д���������ߵİ��������εĸ�������������ż�� ��
���𰸡�
��1���⣺��ͼ1��
����A��x�������ᣬ��B��y�Ḻ������ʱ��
��OC=0D=1��
��������ABCD�ı߳�CD= ![]() ����OCD=��ODC=45�㣬
����OCD=��ODC=45�㣬
����A��x�Ḻ���ᡢ��B��y����������ʱ��
��С�����εı߳�Ϊa��
��CL=С�����εı߳�=DK=LK����3a=CD= ![]() ��
��
���a= ![]() ������С�����α߳�Ϊ
������С�����α߳�Ϊ ![]() ��
��
��һ�κ���y=x+1ͼ��İ��������εı߳�Ϊ ![]() ��
�� ![]()
��2���⣺��ͼ2����DE��CF�ֱ�ֱ��x��y�ᣬ

��֪��ADE�ա�BAO�ա�CBF
��ʱ��m��2��DE=OA=BF=m��OB=CF=AE=2��m��
��OF=BF+OB=2��
��C��������2��m��2����
��2m=2��2��m�������m=1��
�����������Ľ���ʽΪy= ![]() ��
��
��3����3,4��,y=�� ![]() x2+
x2+ ![]() ,ż��
,ż��
���������⣺��3��ʵ������������߿������ϵ���������У���һ���㶼�ڣ�3��4������࣬����������ʱ����һ�㶼�ڣ�3��4�����Ҳ࣬�������������Բ�����
�ٵ���A��x���������ϣ���B��y���������ϣ���C����Ϊ��3��4��ʱ������һ������Ϊ��4��1������Ӧ�ĺ�������ʽ��y=�� ![]() x2+
x2+ ![]() ��
��
�ڵ���A��x ���������ϣ��� B�� y���������ϣ���D ����Ϊ��3��4��ʱ�������ڣ�
�۵���A �� x ���������ϣ��� B�� y�Ḻ�����ϣ���C ����Ϊ��3��4��ʱ��������
�ܵ���A��x ���������ϣ���B��y�Ḻ�����ϣ���D����Ϊ��3��4��ʱ������һ������CΪ����1��3������Ӧ�ĺ����Ľ���ʽ��y= ![]() x2+
x2+ ![]() ��
��
�ݵ���A��x�Ḻ�����ϣ���B��y�Ḻ�����ϣ���D����Ϊ��3��4��ʱ����һ������C�������ǣ�7����3��ʱ����Ӧ�ĺ�������ʽ��y=�� ![]() ��
��
����A��x�Ḻ�����ϣ���B��y�Ḻ�����ϣ���C����Ϊ��3��4��ʱ����һ������D�������ǣ���4��7��ʱ����Ӧ��������Ϊy= ![]() x2+
x2+ ![]() ��
��
���������ߵİ��������εĶ���֪��һ�����������������������Σ��dzɶԳ��ֵģ�
����������κ������ߵİ��������θ���Ϊż����
�����㾫����ͨ��������������ε����ʣ������������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������μ����Խ����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�