题目内容
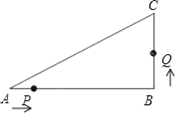
【题目】如图，已知在△ABC中，∠B=90°，AB=8cm，BC=6cm，点P开始从点A开始沿△ABC的边做逆时针运动，且速度为每秒1cm，点Q从点B开始沿△ABC的边做逆时针运动，且速度为每秒2cm，他们同时出发，设运动时间为t秒．
（1）出发2秒后，求PQ的长；
（2）在运动过程中，△PQB能形成等腰三角形吗？若能，则求出几秒后第一次形成等腰三角形；若不能，则说明理由；
【答案】（1）
.
（2）能.当
时.
【解析】
（1）利用勾股定理，根据题意求出PB和BQ的长，再由PB和BQ可以求得PQ的长；
（2）由题意可知P、Q两点是逆时针运动，则第一次形成等腰三角形是PB=QB，再列式即可得出答案.
（1）由题意可得
，
，
因为t=2，所以
，
，
则由勾股定理可得
.
（2）能.由题意可得，，又因为题意可知P、Q两点是逆时针运动，则第一次第一次形成等腰三角形是PB=QB，所以
,即当时，第一次形成等腰三角形.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
