Question

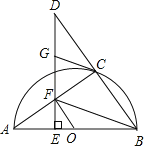
【题目】如图，以等边三角形ABC的BC边为直径画半圆，分别交AB、AC于点E、D，DF是圆的切线，过点F作BC的垂线交BC于点G．若AF的长为2，则FG的长为 ．

Answer 1

【答案】3

【解析】

试题分析：连结OD，作DH⊥FG于H，DM⊥BC于M，根据等边三角形的性质得∠A=∠C=∠ABC=60°，AC=BC，根据切线的性质得OD⊥DF，再证明OD∥AB，则DF⊥AB，在Rt△ADF中根据含30度的直角三角形三边的关系得DF=AF=2，由BC为⊙O的直径，根据圆周角定理得∠BDC=90°，则AD=CD=4，OD=4，所以OM=OD=2，在Rt△DFH中可计算出FH=，DH=FH=3，则GM=3，于是OG=GM﹣OM=1，BG=OB﹣OG=3，在Rt△BGF中可计算FG=BG=3．

解：连结OD，作DH⊥FG于H，DM⊥BC于M，如图，

∵△ABC为等边三角形，

∴∠A=∠C=∠ABC=60°，AC=BC，

∵DF是圆的切线，

∴OD⊥DF，

∵△ODC为等边三角形，

∴∠ODC=60°，

∴∠A=∠ODC，

∴OD∥AB，

∴DF⊥AB，

在Rt△ADF中，AF=2，∠A=60°，

∴AD=4，DF=AF=2，

∵BC为⊙O的直径，

∴∠BDC=90°，

∴BD⊥AC，

∴AD=CD=4，

∴OD=4，

∴OM=OD=2，

在Rt△DFH中，∠DFH=60°，DF=2，

∴FH=，DH=FH=3，

∴GM=3，

∴OG=GM﹣OM=1，

∴BG=OB﹣OG=3，

在Rt△BGF中，∠FBG=60°，BG=3，

∴FG=BG=3．

故答案为3．